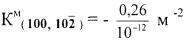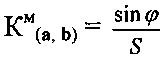Результат интеллектуальной деятельности: Способ диагностики римановой кривизны решетки нанотонких кристаллов
Вид РИД
Изобретение
Изобретение относится к области электронно-микроскопической диагностики реальной структуры нанотонких кристаллов и может быть использовано для диагностики римановой кривизны решетки нанотонких кристаллов.
Известен способ измерения кривизны монокристаллических пластин. Сущность данного изобретения заключается в следующем: для измерения кривизны монокристаллической пластины формируют два параллельных монохроматических рентгеновских луча. Данные лучи направляют на исследуемую пластину, определяют разность углов отражения этих лучей от различных, отстоящих друг от друга на заданном расстоянии точек изогнутой поверхности, при последовательном выведении их в отражающее положение. Одновременно с первыми двумя лучами параллельно и на равном расстоянии от каждого из них формируют и направляют на исследуемую поверхность третий центральный луч, по отражению которого ориентируют пластину перед измерением кривизны. Затем дважды проводят определение разности углов отражения лучей, не совпадающих с центральным, до и после поворота пластины на 180° вокруг оси вращения, лежащей в плоскости прохождения лучей и совпадающей с нормалью к поверхности в точке отражения центрального луча. Кривизну определяют по формуле: К=(Δϕ0+Δϕ180)/2S, где К - кривизна пластины (К=1/R, R - радиус кривизны); S - расстояние между лучами на отражающей поверхности; Δϕ0 и Δϕ180 - соответственно разность углов отражения до и после поворота пластины на 180° вокруг нормали к поверхности в точке отражения центрального луча (RU 2071049, МПК G01N 23/20, 1996 г.).
Недостатком известного способа является невозможность определения римановой кривизны исследуемого объекта.
Известен способ диагностики римановой кривизны решетки кристаллов методом рентгеноструктурного анализа. Сущность данного способа заключается в том, что для диагностики римановой кривизны решетки исследуемого кристаллического объекта используют размытие дифракционных рефлексов на дифракционной картине рентгеновских лучей, полученной методом Лауэ, которое связывают с тензором кривизны Римана-Кристоффеля кристаллической решетки по формуле: 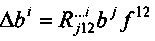 (i, j=1, 2, 3), где Δbi - приращение вектора bi в направлении, перпендикулярном направлению bi;
(i, j=1, 2, 3), где Δbi - приращение вектора bi в направлении, перпендикулярном направлению bi; 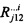 - тензор кривизны Римана-Кристоффеля решетки кристалла; bi - вектор обратной решетки;
- тензор кривизны Римана-Кристоффеля решетки кристалла; bi - вектор обратной решетки; 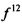 - бесконечно малая площадь поверхности кристалла, от которой получена дифракционная картина (Введение в микромеханику / Под ред. М. Онами. Пер. с англ. П.Д. Баева под ред. Г.Я. Гуна. М.: Металлургия, 1987, с. 235-241, 280 с.).
- бесконечно малая площадь поверхности кристалла, от которой получена дифракционная картина (Введение в микромеханику / Под ред. М. Онами. Пер. с англ. П.Д. Баева под ред. Г.Я. Гуна. М.: Металлургия, 1987, с. 235-241, 280 с.).
Недостатками известного способа являются: низкая точность определения римановой кривизны решетки кристалла, обусловленная большей кривизной сферы Эвальда для рентгеновского излучения; отсутствие надежного способа установления непрерывности разориентации решетки кристалла с помощью анализа непрерывности размытия дифракционного рефлекса; низкая точность определения площади участка кристалла, от которого получают дифракционную картину.
Наиболее близким к заявляемому способу является способ диагностики римановой кривизны решетки кристаллов с использованием просвечивающей электронной микроскопии и электронографии. Данный способ заключается в том, что для диагностики римановой кривизны решетки исследуемого кристалла используют размытие дифракционного рефлекса на микроэлектронограмме, обусловленное римановой кривизной решетки кристалла, получая численное значение средней римановой кривизны решетки кристалла по формуле:
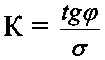 , где ϕ - угол размытия рефлекса; σ - площадь участка кристалла, от которого получена микроэлектронограмма (Малков А.В., Малков В.Б. Реальная структура тонких кристаллов селена. Lambert Academic Publishing (LAP), 2012 г., 189 с.).
, где ϕ - угол размытия рефлекса; σ - площадь участка кристалла, от которого получена микроэлектронограмма (Малков А.В., Малков В.Б. Реальная структура тонких кристаллов селена. Lambert Academic Publishing (LAP), 2012 г., 189 с.).
Недостатками известного способа являются: отсутствие надежного способа установления непрерывности разориентации решетки кристалла путем анализа непрерывности азимутального размытия дифракционного рефлекса, без анализа непрерывности изгибного экстинкционного контура на электронно-микроскопическом изображении кристалла, соответствующем данному рефлексу; низкая точность определения римановой кривизны решетки кристалла, обусловленная определением площади участка кристалла σ, «вырезаемого» селекторной диафрагмой, имеющей неправильную форму; низкая точность определения римановой кривизны решетки кристалла, обусловленная неточным определением угла азимутального размытия рефлекса ϕ и отсутствием цифровых измерений угла размытия рефлекса (измерений, при которых указание числового значения результата измерения угла размытия реализуется путем его цифрового представления; в нашем случае с использованием графического редактора Adobe Photoshop); низкая точность определения римановой кривизны решетки кристалла позволяет определять среднюю риманову кривизну решетки кристалла; отсутствие двумерного направления, в котором определяется риманова кривизна решетки кристалла; низкая экспрессность диагностики римановой кривизны решетки кристалла, обусловленная отсутствием цифровых измерений угла размытия рефлекса на микроэлектронограмме; невозможность определения численных значений римановой кривизны решетки нанотонкого кристалла in situ (т.е. определение численных значений римановой кривизны решетки нанотонкого кристалла в процессе проведения электронно-микроскопических исследований).
Задачей предлагаемого технического решения является разработка более надежного, точного и экспрессного способа диагностики римановой кривизны решетки нанотонкого кристалла.
Поставленная задача решена в предлагаемом способе диагностики римановой кривизны решетки нанотонкого кристалла путем получения электронно-микроскопического изображения нанотонкого кристалла в светлом поле, получения микроэлектронограммы от кристалла, микродифракционного исследования нанотонкого кристалла, анализа ротационного искривления решетки нанотонкого кристалла, отличающемся тем, что на электронно-микроскопическом изображении нанотонкого кристалла выбирают физическую точку М и двумерное направление, для этого выбирают пару - нелинейный изгибной экстинкционный контур и соответствующий ему рефлекс на микроэлектронограмме, испытывающий азимутальное размытие; проводят диагностику римановой геометрии решетки нанотонкого кристалла в данной точке М и данном двумерном направлении, задаваемом бивектором (а, b) - парой неколлинеарных векторов, исходящих из одной точки, совпадающей с центром микроэлектронограммы, полученной от нанотонкого кристалла, расположенных в плоскости микроэлектронограммы, где вектор b соответствует размытому рефлексу, путем совместного анализа пары - нелинейного изгибного экстинкционного контура, присутствующего на электронно-микроскопическом изображении кристалла в темном поле, и соответствующего ему рефлекса на микроэлектронограмме от кристалла, для установления непрерывности азимутального размытия рефлекса и непрерывности соответствующего ему изгибного контура, затем проводят диагностику римановой кривизны решетки нанотонкого кристалла путем определения численного значения римановой кривизны решетки нанотонкого кристалла в данной точке М и данном двумерном направлении, задаваемом бивектором (а, b), по формуле:
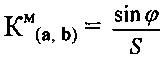 ,
,
где КМ(a, b) - риманова кривизна решетки нанотонкого кристалла в данной точке М - физической «точке» кристалла и данном двумерном направлении, задаваемом бивектором (а, b); ϕ - угол азимутального размытия рефлекса, определяемый с помощью цифровых измерений; S - площадь физической точки M - участка нанотонкого кристалла, охватывающая нелинейный изгибной экстинкционный контур, соответствующий рефлексу с непрерывным азимутальным размытием, определяемая в темном поле.
Заявленный способ диагностики римановой кривизны решетки нанотонкого кристалла в данной точке и данном двумерном направлении заключается в следующем: для диагностики римановой кривизны решетки исследуемого кристалла используют азимутальное размытие дифракционного рефлекса на микроэлектронограмме, анализируя непрерывность размытия рефлекса путем анализа размытия и рефлекса, и непрерывности изгибного контура, соответствующего рефлексу, в темном поле. Азимутальное непрерывное размытие дифракционного рефлекса обусловлено римановой геометрией и римановой кривизной решетки нанотонкого кристалла (Введение в микромеханику / Под ред. М. Онами. Пер. с англ. П.Д. Баева под ред. Г.Я. Гуна. М.: Металлургия, 1987, с. 235-241, 280 с.) в данной точке M и данном двумерном направлении. Двумерное направление задается бивектором (а, b) - парой неколлинеарных векторов а и b, исходящих из одной точки, совпадающей с центром микроэлектронограммы (фиг. 2), и расположенных в плоскости микроэлектронограммы, при этом вектор b соответствует размытому рефлексу. Численное значение римановой кривизны решетки кристалла получают по формуле (1), при этом:
1) диагностируют риманову геометрию решетки нанотонкого кристалла в точке M и данном двумерном направлении, выбирая пару - нелинейный изгибной экстинкционный контур и соответствующий ему рефлекс, испытывающий азимутальное размытие на микроэлектронограмме, и с этой целью анализируют непрерывность разориентации решетки нанотонкого кристалла в данной точке и данном двумерном направлении путем совместного анализа непрерывности размытия рефлекса на микроэлектронограмме от кристалла и непрерывности соответствующего данному рефлексу нелинейного изгибного экстинкционного контура на электронно-микроскопическом изображении кристалла в темном поле, устанавливая непрерывность разориентации решетки нанотонкого кристалла в данной точке и данном двумерном направлении и, соответственно, диагностируя геометрию решетки кристалла в точке M и данном двумерном направлении, задаваемом бивектором (а, b), как риманову геометрию;
2) диагностируют риманову кривизну решетки нанотонкого кристалла в данной точке и данном двумерном направлении путем:
2.1) определения численного значения угла ϕ - угла азимутального размытия рефлекса на микроэлектронограмме от кристалла, путем цифровых измерений in situ;
2.2) определения численного значения площади физической «точки» M - участка кристалла, охватывающего нелинейный изгибной контур, соответствующий выбранному рефлексу с непрерывным азимутальным размытием (непрерывной азимутальной разориентацией) в темном поле;
2.3) определения численного значения римановой кривизны решетки нанотонкого кристалла в данной точке и данном двумерном направлении, задаваемом бивектором (а, b), по формуле (1).
Технический результат, достигаемый предлагаемым способом, заключается в том, что диагностика римановой кривизны решетки нанотонкого кристалла выполняется надежным, точным и экспрессным способом.
Надежность предлагаемого способа диагностики римановой кривизны решетки нанотонких кристаллов обусловлена определением непрерывности разориентации решетки кристалла не только по непрерывности размытия рефлекса на микроэлектроннограмме, но и по данному рефлексу изгибного экстинкционного контура на электронно-микроскопическом изображении кристалла.
Точность предлагаемого способа диагностики римановой кривизны решетки нанотонких кристаллов обусловлена точностью определения численного значения угла азимутального размытия рефлекса ϕ на микроэлектронограмме от кристалла, цифровым методом и точностью определения численного значения площади физической «точки» M нанотонкого кристалла - участка кристалла, охватывающего нелинейный, изгибной, экстинкционный контур, соответствующий рефлексу с азимутальным размытием, а не площади участка кристалла, «вырезаемой» селекторной диафрагмой, имеющей неправильную форму.
Экспрессность предлагаемого способа диагностики римановой кривизны решетки нанотонких кристаллов обусловлена экспрессностью определения численных значений угла азимутального размытия рефлекса ϕ на микроэлектронограмме от кристалла, с помощью цифровых измерений in situ; и экспрессностыо определения численного значения площади физической «точки» M нанотонкого кристалла S участка кристалла, охватывающего нелинейный, изгибной, экстинкционный контур, соответствующий выбранному рефлексу, с непрерывным азимутальным размытием (непрерывной азимутальной разориентацией), в темном поле.
Вместе с тем, при диагностике римановой кривизны решетки нанотонкого кристалла предлагаемым способом указывается не только физическая «точка» M нанотонкого кристалла, но и двумерное направление, задаваемое бивектором (а, b), где вектор b на микроэлектронограмме соответствует рефлексу с азимутальным размытием.
Численное значение римановой кривизны решетки нанотонкого кристалла в данной точке и данном двумерном направлении, задаваемом бивектором (а, b), определяется по формуле (1).
Предлагаемый способ иллюстрируется следующим примером.
Пример 1
При температуре изотермического отжига 150°С в аморфных пленках селена растут ромбовидные кристаллы, на электронно-микроскопическом изображении которых наблюдается нелинейная веерообразная система изгибных контуров (фиг. 1а, б). На фиг. 1(а, б) представлено электронно-микроскопическое изображение нанотонкого кристалла гексагонального селена с нелинейной системой изгибных экстинкционных контуров: а) в светлом поле и б) в темном поле в рефлексе (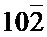 ). Микроэлектронограмма от центра кристалла с нелинейной системой изгибных экстинкционных контуров (фиг. 1а) и с непрерывноразмытым рефлексом (
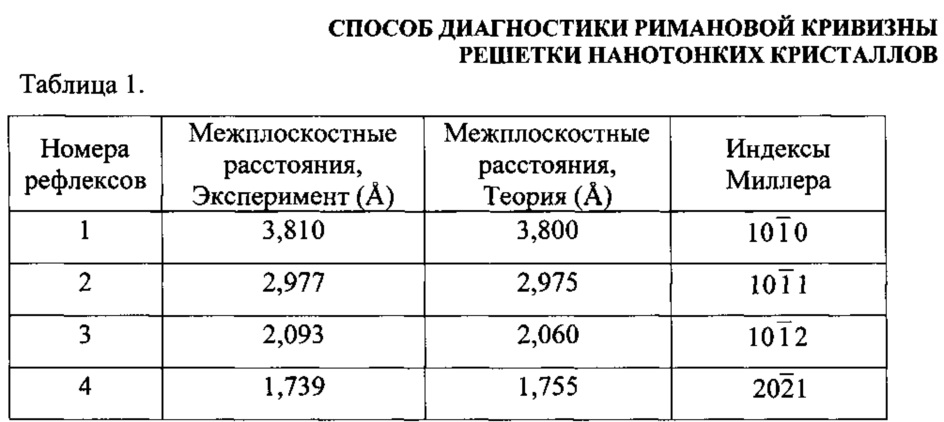
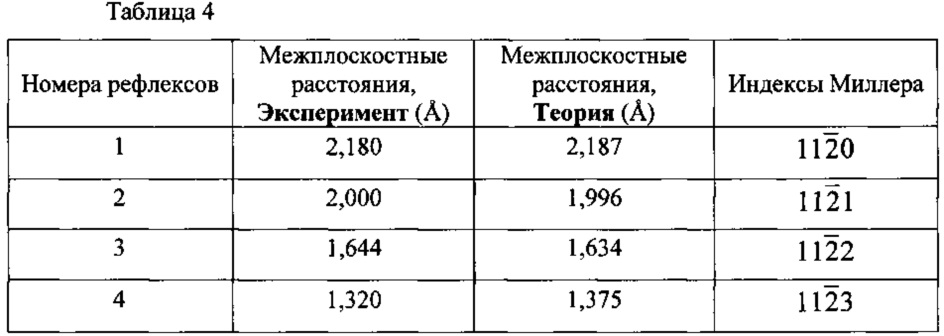
). Микроэлектронограмма от центра кристалла с нелинейной системой изгибных экстинкционных контуров (фиг. 1а) и с непрерывноразмытым рефлексом (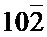 ) представлена на (фиг. 2), на которой приведены номера рефлексов (1-4), полученные при просвете от плоскостей кристаллической решетки. Результаты расчета индексов Миллера приведены в таблице 1.
) представлена на (фиг. 2), на которой приведены номера рефлексов (1-4), полученные при просвете от плоскостей кристаллической решетки. Результаты расчета индексов Миллера приведены в таблице 1.
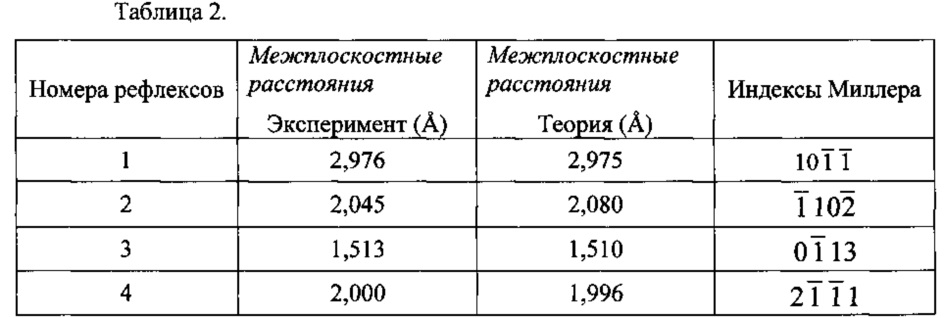
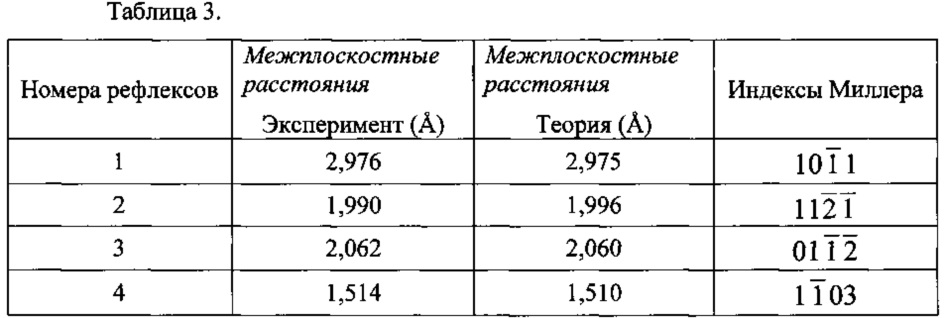
На фиг. 3 представлены результаты микродифракционного исследования данного нанотонкого кристалла. На фиг. 3а, б представлены микроэлектронограммы от периферийных участков ромбовидного кристалла с нелинейной веерообразной картиной системы изгибных контуров на электронно-микроскопическом изображении. На фиг. 3в представлена микроэлектронограмма от "левой" периферийной части ромбовидного кристалла после поворота кристалла вокруг длинной диагонали. На микроэлектронограммах (фиг. 3а, б) от периферийных участков ромбовидного кристалла с нелинейной веерообразной картиной системой изгибных контуров на электронно-микроскопическом изображении приведены номера рефлексов (1-4) в соответствии с таблицами 2, 3. На микроэлектронограмме (фиг. 3в) от «левой» периферийной части ромбовидного кристалла после поворота кристалла вокруг длинной диагонали приведены номера рефлексов (1-4) в соответствии с таблицей 4. Расчет межплоскостных расстояний для данных микроэлектронограмм приведен в таблицах 2, 3 и 4. Таблица 2 соответствует микроэлектронограмме, полученной от «правого» участка кристалла, относительно плоскости симметрии, проходящей через короткую диагональ ромба перпендикулярно поверхности кристалла (фиг. 3б). Таблица 3 соответствует микроэлектронограмме, полученной от «левого» участка кристалла, относительно плоскости симметрии, проходящей через короткую диагональ ромба перпендикулярно поверхности кристалла (фиг. 3а). Таблица 4 соответствует микроэлектронограмме от «левой» периферийной части ромбовидного кристалла после поворота кристалла вокруг длинной диагонали (фиг. 3в). Сравнение микроэлектронограмм от "правой" части и центра кристалла (фиг. 3б и фиг. 2) показывает, что общими для них являются рефлексы 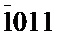 и
и 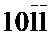 . Рефлексы
. Рефлексы 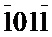 и
и 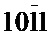 являются общими для микроэлектронограмм от "левой" части (фиг. 3а) и центра кристалла (фиг. 2).
являются общими для микроэлектронограмм от "левой" части (фиг. 3а) и центра кристалла (фиг. 2).
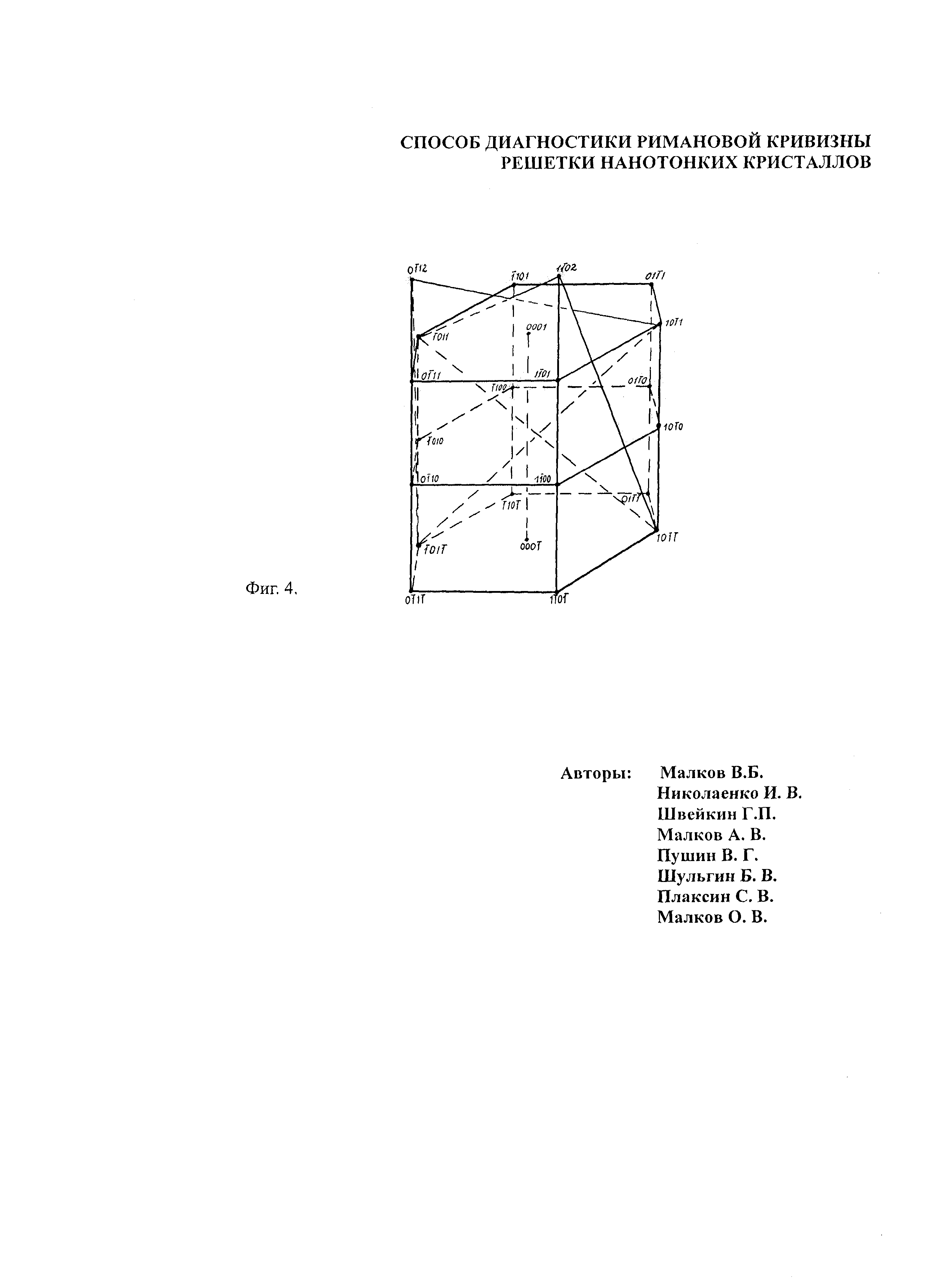
В соответствии с данными фактами ротационное искривление решетки в "правой" части кристалла можно интерпретировать как вращение обратной решетки вокруг направления, проходящего через узлы обратной решетки гексагонального селена с индексами 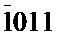 ,
,  , а ротационное искривление решетки в "левой" части кристалла - как вращение обратной решетки вокруг направления, проходящего через узлы с индексами
, а ротационное искривление решетки в "левой" части кристалла - как вращение обратной решетки вокруг направления, проходящего через узлы с индексами 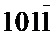 и
и 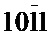 (фиг. 4).
(фиг. 4).
Вращение обратной решетки вокруг данных направлений является суммой двух составляющих: вращения обратной решетки вокруг направления, проходящего через узлы с индексами 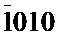 ,
, 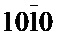 , и вращения обратной решетки вокруг [001] (фиг. 4). При этом вращение вокруг [001] происходит в противоположных направлениях в "правой" и "левой" частях кристалла, а вращение вокруг направления, проходящего через узлы обратной решетки с индексами
, и вращения обратной решетки вокруг [001] (фиг. 4). При этом вращение вокруг [001] происходит в противоположных направлениях в "правой" и "левой" частях кристалла, а вращение вокруг направления, проходящего через узлы обратной решетки с индексами 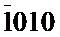 ,
, 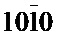 , - в одном и том же направлении.
, - в одном и том же направлении.
Изгиб решетки кристалла селена вокруг [001] является вогнутым (Bolotov I.Ε., Kolosov V. Yu. and Malkov V.В. Electron Microscopy Investigation of Crystals Based on Bend-Contour Arrangement 3. Formation of Subgrain Boundaries in Dislocation-Free Crystals of Selenium // Phys. Stat. Sol. (a). 1986. V. 95. P. 377-383). Установим, каким - вогнутым или выпуклым - является изгиб решетки кристалла (фиг. 1) вокруг направления, совпадающего с длинной диагональю ромбовидного кристалла. Пусть изгиб решетки кристалла (фиг. 1) вокруг указанного направления является выпуклым. Тогда после поворота ромбовидного кристалла вокруг длинной диагонали в направлении, противоположном направлению раскрытия веера изгибных контуров на угол 25°, в «левом» периферийном участке кристалла, в отражающем положении должны оказаться призматические плоскости второго рода. Микроэлектронограмма от «левого» периферийного участка повернутого нанотонкого кристалла показана на фиг. 3в. Результаты расчета микроэлектронограммы приведены в таблице 4. В отражающем положении находятся призматические плоскости второго рода. Отсюда следует вывод: изгиб решетки кристалла (фиг. 1) вокруг направления, совпадающего с длинной диагональю ромбовидного кристалла, является выпуклым.
Таким образом, исследование реальной структуры нанотонкого кристалла (фиг. 1), проведенное с помощью метода микродифракции, позволяет установить: решетка нанотонкого кристалла с нелинейной веерообразной картиной изгибных экстинкционных контуров на электронно-микроскопическом изображении искривлена ротационным образом вокруг двух взаимно перпендикулярных направлений. Во-первых, вокруг оси “С” (вогнутый) и, во-вторых, вокруг перпендикулярного ей направления, совпадающего с длинной диагональю ромбовидного кристалла (выпуклый).
Геометрия поверхности, изогнутой вокруг двух взаимно перпендикулярных направлений, представляет собой двумерное риманово пространство и, соответственно, ее геометрия является римановой.
Геометрия решетки нанотонких кристаллов с нелинейной системой изгибных экстинкционных контуров на их электронно-микроскопическом изображении, испытывающей упругое ротационное искривление вокруг двух взаимно перпендикулярных направлений, является римановой, так как и кристаллографические плоскости кристалла искривлены вокруг двух взаимно перпендикулярных направлений.
Выбор и анализ пары - нелинейного изгибного контура на электронно-микроскопическом изображении нанотонкого кристалла (фиг. 1) и рефлекса на микроэлектронограмме (фиг. 2), полученной от нанотонкого кристалла, позволяет сделать вывод: геометрия решетки данного нанотонкого кристалла является римановой и, соответственно, риманова кривизна решетки такого кристалла отлична от нуля. Действительно, рефлекс (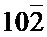 ) на электронограмме от кристалла (фиг. 2) испытывает непрерывное азимутальное размытие и соответствующий ему изгибной контур с индексом (
) на электронограмме от кристалла (фиг. 2) испытывает непрерывное азимутальное размытие и соответствующий ему изгибной контур с индексом (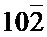 ) на электронно-микроскопическом изображении кристалла в темном поле (фиг. 1б) является непрерывным нелинейным изгибным контуром.
) на электронно-микроскопическом изображении кристалла в темном поле (фиг. 1б) является непрерывным нелинейным изгибным контуром.
Таким образом, все признаки римановой геометрии решетки нанотонкого кристалла выполняются для кристалла, представленного на фиг. 1, и, следовательно, можно диагностировать геометрию решетки данного кристалла как риманову геометрию.
После диагностики римановой геометрии решетки нанотонкого кристалла выполним диагностику римановой кривизны решетки нанотонкого кристалла в данной точке и данном двумерном направлении. «Точка» М, в которой диагностируется риманова кривизна решетки нанотонкого кристалла, является областью (фиг. 6), ограничивающей изгибной экстинкционный контур (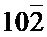 ) (фиг. 1б). На фиг. 6 показана область в виде прямоугольника (показана стрелкой), выделяющая нелинейный изгибной экстинкционный контур, соответствующий азимутально размытому рефлексу (
) (фиг. 1б). На фиг. 6 показана область в виде прямоугольника (показана стрелкой), выделяющая нелинейный изгибной экстинкционный контур, соответствующий азимутально размытому рефлексу (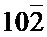 ) на микроэлектронограмме, полученной от кристалла, принимаемая за физическую точку М. Данная «точка» является физической точкой, то есть фактически областью, вокруг которой по замкнутому контуру происходит параллельный перенос вектора
) на микроэлектронограмме, полученной от кристалла, принимаемая за физическую точку М. Данная «точка» является физической точкой, то есть фактически областью, вокруг которой по замкнутому контуру происходит параллельный перенос вектора 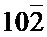 . Так как истинные размеры данной области малы, название данной области - точка - вполне оправдано.
. Так как истинные размеры данной области малы, название данной области - точка - вполне оправдано.
Двумерное направление определяется бивектором (001, 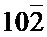 ), т.е. парой неколлинеарных векторов, исходящих из одной точки, совпадающей с центром микроэлектронограммы (фиг. 2), и расположенных в плоскости микроэлектронограммы, при этом вектор
), т.е. парой неколлинеарных векторов, исходящих из одной точки, совпадающей с центром микроэлектронограммы (фиг. 2), и расположенных в плоскости микроэлектронограммы, при этом вектор 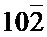 соответствует размытому рефлексу (
соответствует размытому рефлексу (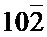 ).
).
Непрерывность азимутального размытия рефлекса (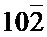 ) (фиг. 2) и непрерывность соответствующего ему изгибного экстинкционного контура на электронно-микроскопическом изображении нанотонкого кристалла в темном поле (фиг. 1б) указывают на непрерывность разориентации решетки нанотонкого кристалла в данной точке М (фиг. 6) и данном двумерном направлении (001,
) (фиг. 2) и непрерывность соответствующего ему изгибного экстинкционного контура на электронно-микроскопическом изображении нанотонкого кристалла в темном поле (фиг. 1б) указывают на непрерывность разориентации решетки нанотонкого кристалла в данной точке М (фиг. 6) и данном двумерном направлении (001, 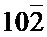 ), что позволяет диагностировать геометрию решетки нанотонкого кристалла в точке М и двумерном направлении, задаваемом бивектором (001,
), что позволяет диагностировать геометрию решетки нанотонкого кристалла в точке М и двумерном направлении, задаваемом бивектором (001, 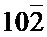 ), как риманову геометрию.
), как риманову геометрию.
Численное значение римановой кривизны решетки нанотонкого кристалла в точке М и в двумерном направлении, задаваемом бивектором (001, 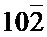 ), определяется по формуле (1).
), определяется по формуле (1).
На фиг. 5 изображено цифровое измерение угла азимутального размытия рефлекса (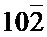 ) на микроэлектронограмме, полученной от кристалла, представленного на электронно-микроскопическом изображении на фиг. 1. Значение угла азимутального размытия рефлекса (
) на микроэлектронограмме, полученной от кристалла, представленного на электронно-микроскопическом изображении на фиг. 1. Значение угла азимутального размытия рефлекса (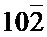 ) на микроэлектронограмме определяется с помощью цифровых измерений in situ и в нашем случае составляет (фиг. 5) ϕ=8,7°. Отсюда sinϕ=0,15.
) на микроэлектронограмме определяется с помощью цифровых измерений in situ и в нашем случае составляет (фиг. 5) ϕ=8,7°. Отсюда sinϕ=0,15.
Площадь S на фиг. 6 вычисленная с учетом увеличения электронно-микроскопического изображения кристалла, равна: S=0,58 мкм2.
Тогда численное значение римановой кривизны решетки в точке М нанотонкого кристалла (фиг. 6) в двумерном направлении (001, 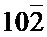 ) равно:
) равно:
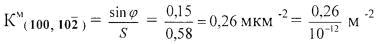
Поскольку изгиб решетки нанотонкого кристалла селена вокруг [001] является вогнутым, а изгиб решетки нанотонкого ромбовидного кристалла (фиг. 1) вокруг направления, совпадающего с длинной диагональю, как было показано выше, является выпуклым, приходим к выводу: знак римановой кривизны решетки в точке М (фиг. 6) нанотонкого кристалла (фиг. 1) в двумерном направлении (001,  ) является отрицательным.
) является отрицательным.
Учитывая знак римановой кривизны решетки кристалла, получаем окончательный результат диагностики римановой кривизны решетки нанотонкого кристалла в точке М (фиг. 6) и двумерном направлении (001,  ):
):