Результат интеллектуальной деятельности: СПОСОБ ВИБРОАКУСТИЧЕСКОЙ ДЕФЕКТОВКИ КОЛЕНЧАТОГО ВАЛА
Вид РИД
Изобретение
Изобретение относится к способам неразрушающего контроля объектов, а именно коленчатого вала автомобильных двигателей.
Распространение усталостных разрушений определяются возвратно-поступательными движениями дислокаций, их взаимодействиями между собой и другими дефектами кристаллической решетки. При этом возникают вакансии, локальное повышение напряжений и температуры, способствующие зарождению трещин.
На основании дислокационных механизмов образования и развития трещин под действием деформаций была предложена модель физического предела усталости (Костецкий Б.И. Надежность и долговечность машин / Б.И. Костецкий, И.Г. Носовский, Л.И. Бершадский, А.К. Караулов. - Киев: Техника, 1975. - 408 с).
Сущность модели: в процессе циклического нагружения при критическом напряжении σ0 в поверхностном слое толщиной 1-3 диаметра зерна происходит поверхностное упрочнение за счет повышения плотности образующихся дислокаций и процесса старения. По мере увеличения числа циклов нагружений и достижения линии образования субмикротрещин происходят скопления дислокаций критической плотности.
Усталостное разрушение является результатом многократно повторенных быстро чередующихся упругих и пластических деформаций, распределяющихся в силу неоднородности материала неравномерно по объему детали. Первичные повреждения возникают в микрообъемах, неблагоприятно ориентированных относительно действия нагрузки, преднапряженных местными дефектами. Постепенно накапливаясь и суммируясь, локальные повреждения дают начало общему разрушению детали.
Следовательно, последовательность модели физического предела усталости такова: дислокации - субмикро - микро - макротрещины - разрушение.
Для определения основных факторов, ограничивающих ресурс коленчатого вала, необходимы значения интенсивности анализируемых процессов и предельные значение параметров технического состояния, которые определяются в процессе их дефектовки.
Усталостные разрушения (трещины) начинаются в области концентраторов напряжений (галтели, отверстия для смазки, грязеуловители). Наиболее часто для коленчатых валов используют магнитную дефектоскопию (Никишин В.Н. Обеспечение качества коленчатого вала автомобильного дизеля / В.Н. Никишин, А.Т. Кулаков, А.С. Денисов, А.А. Видинеев // Вестник Саратовского государственного технического университета, 2006. - №4. - С. 69-76.), которая имеет довольно значительную трудоемкость и субъективность. Виброакустический интегральный способ свободных колебаний активно применяется для обнаружения трещин и других внутренних дефектов для деталей конструкций, изделий из различных материалов, а также для выявления дефектов в рельсах и осях колесной пары. Исследование полученных сигналов осуществляется путем анализа гармонических составляющих акустического сигнала. Необходимо обосновать возможность применения способа, что подразумевает под собой изучение и анализ виброакустических сигналов, полученных при импульсном воздействии на коленчатый вал.
При методическом обосновании применимости виброакустического способа для обнаружения трещин в коленчатом вале необходима идентификация коленчатого вала как динамической системы при ударе, то есть построение соответствующей математической модели, основанной на экспериментальных данных.
Задача настоящего изобретения заключается в создании эффективного способа виброакустической дефектовки коленчатого вала на основе анализа виброакустических сигналов, полученных при импульсном воздействии на коленчатый вал
Решение поставленной задачи позволит выполнить экспресс-анализ коленчатого вала в условиях ремонтных предприятий при ремонте двигателей.
Технический результат заявляемого изобретения заключается в снижении трудоемкости дефектовки и повышении ее объективность.
Поставленная задача решается за счет того, что способ виброакустической дефектовки коленчатого вала, основанный на методике определения добротности коленчатого вала на основании анализа его, как динамической системы, включает следующие этапы: измерение виброакустических колебаний коленчатого вала при импульсном воздействии, применение к полученному виброакустическому сигналу низкочастотной фильтрации, аппроксимация полученной импульсной переходной функции при помощи аналитических выражений, вычисление передаточной функции динамической системы коленчатого вала, построение амплитудно-частотной характеристики динамической системы коленчатого вала по полученной передаточной функции, определение добротности системы по полученной амплитудно-частотной характеристике, сравнение полученной добротности динамической системы коленчатого вала с эталонным бездефектным значением добротности, отбраковка коленчатого вала в случае выявления в нем дефекта и отправка на утилизацию. В случае соответствия добротности рассматриваемого коленчатого вала нормативным значениям, производится его восстановление.
Заявляемое изобретение иллюстрируется чертежами:
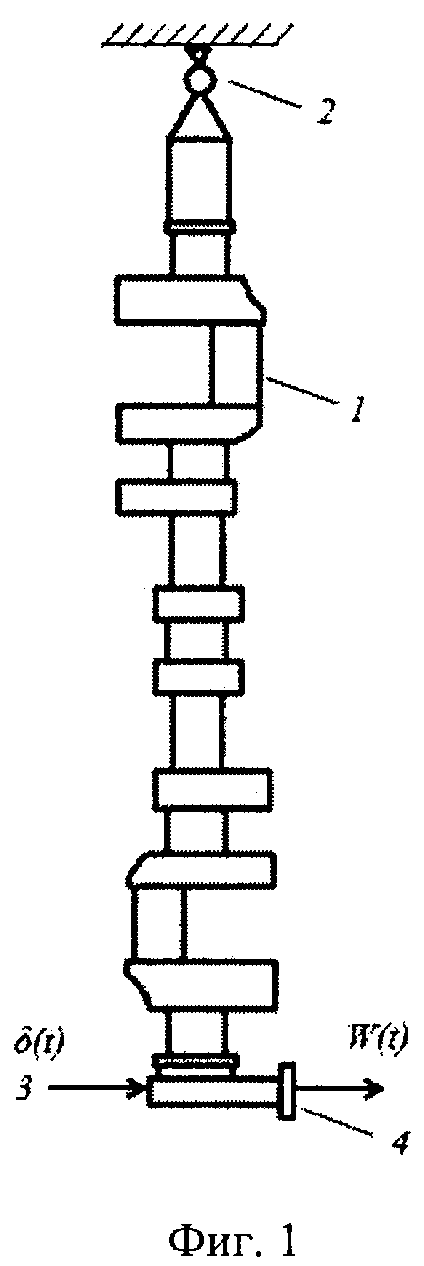
фиг. 1 - возбуждение колебаний в коленчатом вале импульсным воздействием и их прием вибропреобразователем, где позициями обозначены:
1 - коленчатый вал,
2 - подвеска,
3 - боек,
4 - датчик с вибропреобразоввателем.
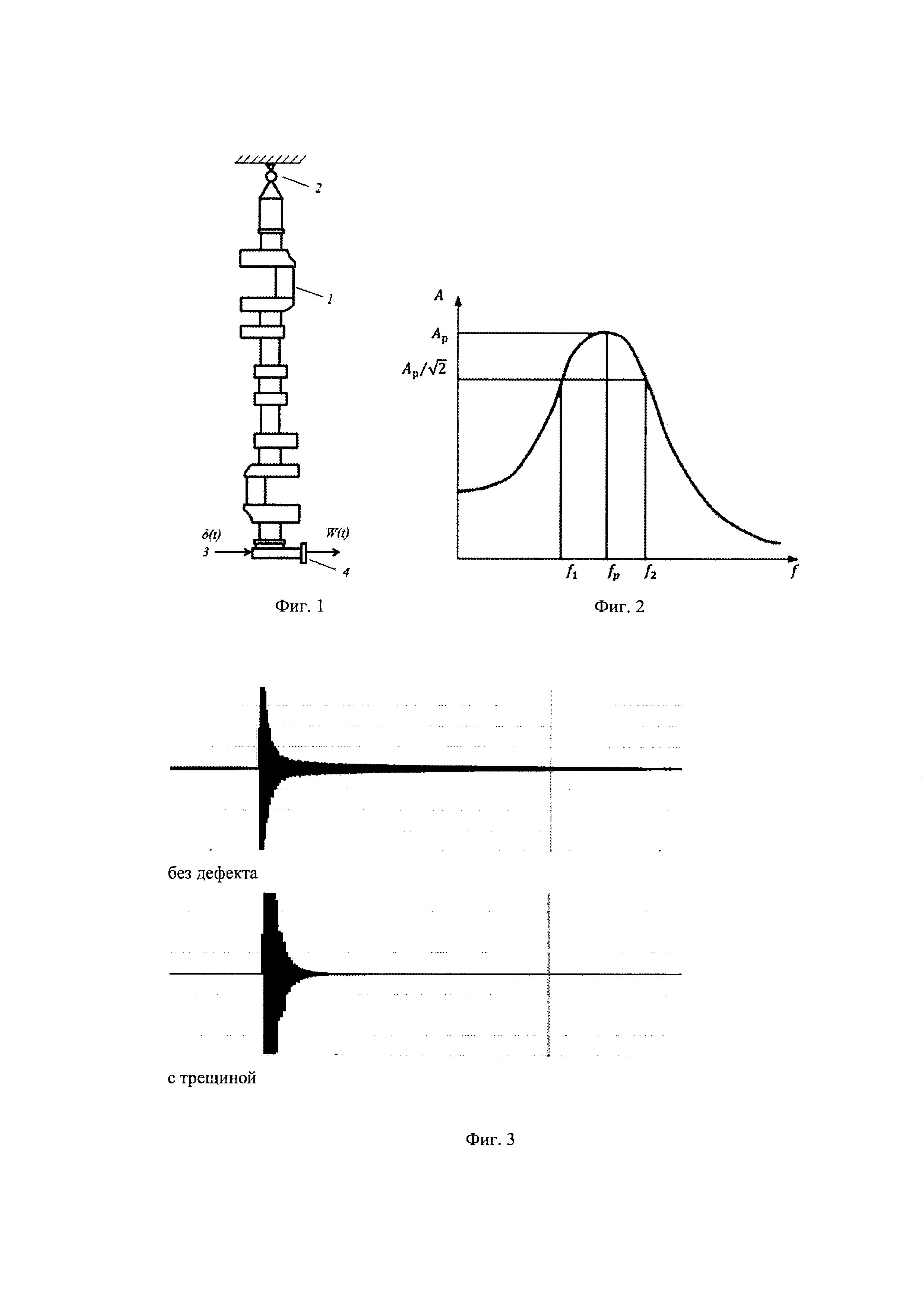
фиг. 2. - определение добротности колебательной системы по резонансной кривой,
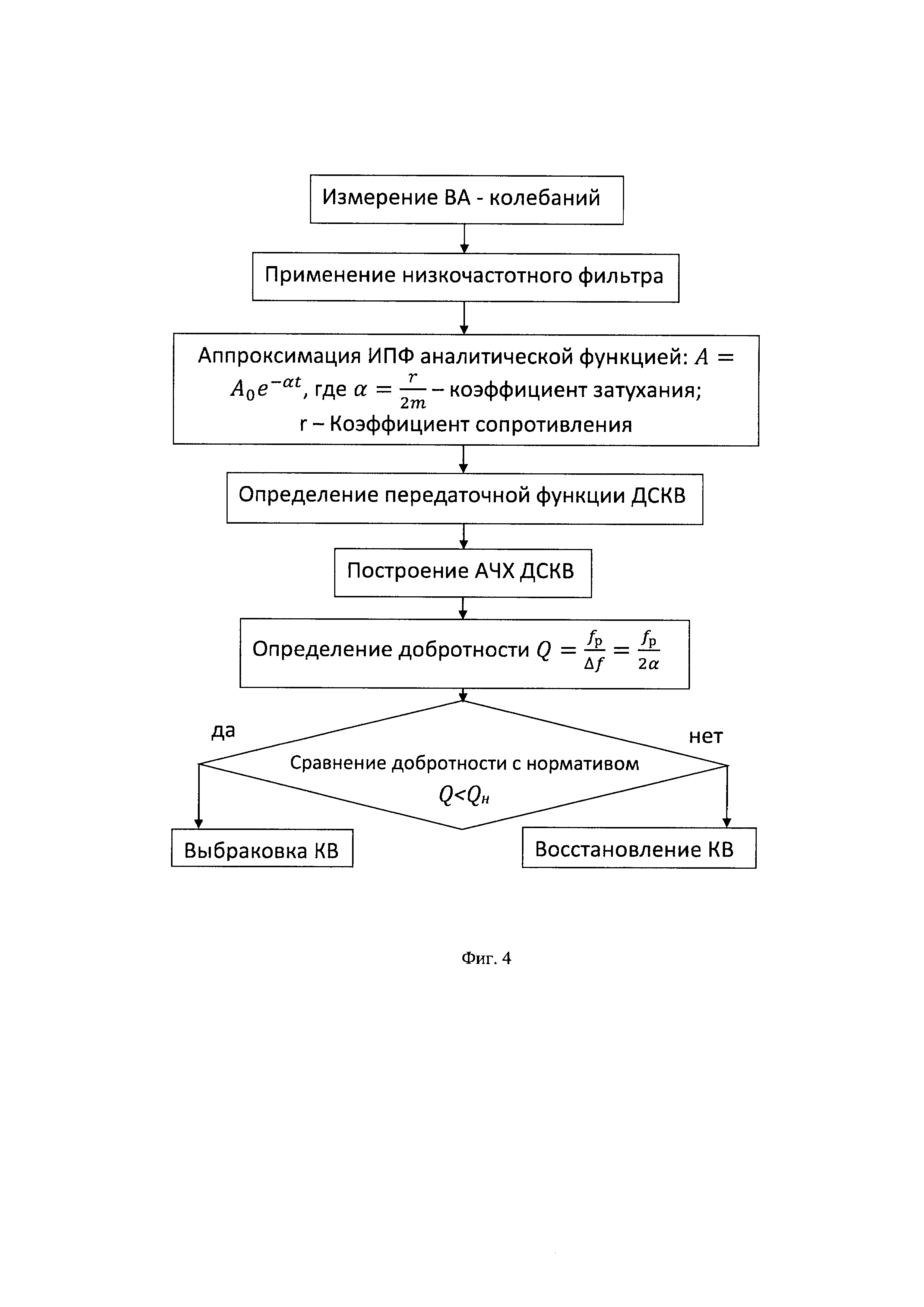
фиг. 3 - импульсная переходная функция для коленчатого вала,
фиг. 4 - алгоритм идентификации динамической системы коленчатого вала и вычисления добротности
При анализе динамической системы коленчатого вала как динамической системы необходимо рассмотреть происходящие в нем колебательные процессы после импульсного воздействия для получения основных информативных параметров. Упругость - это свойство объекта восстанавливать свои форму и объем после прекращения действия внешних сил. Среда, обладающая свойством упругости, называется упругой средой, в которой под действием механических возмущений возникают упругие колебания. Упругие колебания могут также возникать и в механических системах, либо в частях упругой системы, при этом распространяются механические возмущения, которые называются акустическими или упругими волнами.
Акустические колебания и акустические волны активно используются в неразрушающем контроле. Для проведения виброакустического контроля различных объектов используют линейную акустику, то есть деформация пропорциональна приложенной силе.
Для проведения экспериментальных исследования и построения математический модели коленчатого вала, как динамической системы, необходимо рассмотреть начальные предпосылки и ограничения, основанные на известных работах М.Д. Генкина, В.Л. Бидермана, С.А. Добрынина, В.В. Клюева:
1. При анализе свободных колебаний механических систем при импульсном воздействии значение имеют измерения вблизи резонансной частоты.
2. При ударе возмущающие силы возникают в результате взаимодействия соударяющихся объектов и могут быть найдены только в связи с изучением динамической деформации последних. При соударении двух тел (в данном случае бойка и коленчатого вала) их общей деформации можно пренебречь из-за крайней незначительности по сравнению с местной. Вследствие того, что взаимодействие между коленчатым валом и бойком занимает крайне незначительное время (1,5…6 мс) при условии, что время переходного импульсного процесса в нашем случае 160…200 мс, входной импульс силы можно рассматривать как мгновенный
3. Импульс силы при проведении экспериментальных исследований подбирается такой величины, при котором в спектре полученного виброакустического сигнала будет минимум частотных составляющих, при этом стоит помнить, что слабый импульс силы вызовет в коленчатом валу виброакустические колебания малой амплитуды, что не позволит в полной мере оценить качество импульсной переходной функции.
4. Для получения стабильных результатов в одинаковых условиях при проведении экспериментальных исследований необходимо обеспечить минимальную шероховатость поверхности соударяющихся тел.
5. Расположение датчика на объекте контроля при свободных колебаниях при импульсном воздействии не имеет особого значения при наличии местной деформации. Тем не менее, для создания одинаковых условий, датчик располагается под углом 180° по отношению к бойку.
Существует множество путей аппроксимации ударных воздействий классическими функциями. Наиболее часто при описании ударов используется полуволна синусоиды

δ-функция широко используемая для решения задач автоматического управления, также применяется для описания ударных возмущающих воздействий, отвечает условию

При этом спектр δ-функции является постоянной величиной.
На основании приведенной классификации наиболее подходящим для описания удара бойка на поверхность коленчатого вала является применение δ-функции, так как она представляет собой импульс бесконечно малой длины и описывает ударное воздействие с продолжительностью намного меньшей длительности переходного процесса.
Дельта-импульс применяется, когда необходимо произвести описание процессов, протекающих быстро во времени, таких как ударные процессы. При использовании дельта-импульса для описания ударных процессов, описываемая сила за малый промежуток времени возрастает до максимальных значений, а затем, также быстро возвращается к нулевому значению. При этом за время возрастания и убывания силы совершается некоторая работа.
Использование дельта-импульса позволяет производить анализ быстропротекающих процессов. При известной продолжительности сигнала и закона изменения амплитуды с течением времени имеется возможность идентифицировать переходный процесс системы, и, следовательно, получить необходимую информацию о его параметрах. Одним из таких переходных процессов являются собственные колебания KB при воздействии на него импульсным ударным возмущением в виде δ-импульса.
При использовании импульсного возмущающего воздействия на коленчатый вал можно получить импульсную переходную функцию на основании регистрации его свободных виброакустических колебаний. В реальных условиях свободные колебания в объекте протекают под действием сил сопротивления, в результате чего происходит уменьшение амплитуды колебаний. Такие колебания называются затухающими.
Наиболее распространенным является случай, когда скорость движения в упругой среде пропорциональна силе сопротивления [7]:

где r - коэффициент сопротивления, знак минус показывает разнонаправленность скорости  и силы Fc.
и силы Fc.
Рассмотрим точку, совершающую гармонические колебаний в упругой среде, имеющей коэффициент сопротивления r. Запишем уравнение по второму закону Ньютона, описывающее колебания:

где α - коэффициент затухания, определяющий скорость затухания колебательного процесса. С затуханием колебаний, энергия колебательного процесса постепенно убывает.
Уравнение затухающего колебательно процесса может быть представлено в дифференциальной форме:

Одними из основных параметров колебательного процесса являются частота и период. Для затухающих колебаний они будут иметь вид:

При  затухающие колебания являются гармоническими, амплитуда которых изменяется по закону:
затухающие колебания являются гармоническими, амплитуда которых изменяется по закону:

Рассмотренные характеристики колебательного процесса связаны с анализом временной зависимости колебаний, то есть с импульсной переходной функцией. Основной же характеристикой колебательной системы является добротность.

В нашем случае, энергия виброакустических колебаний рассеивается, следовательно, по мере увеличения трещины, рассеивание энергии будет увеличиваться, а добротность кольца снижаться. Добротность механической системы определяется по ее резонансной кривой, или по амплитудно-частотной характеристике.
Для коленчатого вала добротность определяется из амплитудно-частотной характеристики, которую можно получить из передаточной функции. Передаточная функция в свою очередь определяется из импульсной переходной функции. Для определения добротности необходимо определить ширину резонансной кривой, для этого определяют значение, равное отношению максимальное амплитуды к корню из двух, то есть Ар √2. На пересечении резонансной кривой и этого значения определяют границы ширины резонансной кривой ƒ2 и ƒ1. Полученные частоты связаны с шириной следующим соотношением: Δƒ=ƒ2-ƒ1. Добротность определяется как отношение резонансной частоты к ширине резонансной кривой: Q=ƒp/Δƒ
Наличие трещин обуславливает, как известно, повышенное рассеяние энергии виброакустических колебаний. Таким образом, добротность является показателем качества динамической системы, который зависит от основных ее характеристик, таких как резонансная частота и декремент затухания. Следовательно, добротность может служить идентификатором состояния коленчатого вала. Идентификация математической модели коленчатого вала, как динамической системы при импульсном воздействии, представляет определение добротности. Рассмотрим коленчатый вал как динамическую систему, у которой имеется входное воздействие, осуществляемое бойком, регистрируется вибродатчиком выходное воздействие, а сам коленчатый вал закреплен на подвеске. При ударе бойком, входное воздействие, с точки зрения теории автоматического управления, можно рассматривать как дельта-импульс, а выходное как импульсную переходную функцию w(t). На основании импульсной переходной функции можно получить передаточную функцию динамической системы коленчатого вала, по которой определяется параметр, позволяющий однозначной идентифицировать состояние объекта контроля на наличие дефектов, а именно добротность. Добротность напрямую связана с частотой собственных колебаний коленчатого вала и коэффициентом затухания колебаний.
Типичная импульсная переходная функция для коленчатого вала без дефекта и с трещиной представлены на фиг. 3.
Данная импульсная переходная функция описывается выражением:

где α - коэффициент затухания, ω0 - частота колебаний системы, а0 - начальная амплитуда переходного процесса. Применяя преобразование Лапласа к импульсной переходной функции (8), получим передаточную функцию KB как динамической системы:

Введем замену  получим
получим

Далее определяем амплитудно-частотную характеристику (АЧХ) динамической системы к по формуле:

тогда 
На основании полученной амплитудно-частотной характеристики строится график и определяется добротность динамической системы. На основании амплитудно-частотной характеристики определяется добротность (Q=ƒp/(ƒ2-ƒ1)=ƒр/Δƒ). Таким образом, получена передаточная функция коленчатого вала, как динамической системы. Значение параметров k, Т, γ зависят от размеров, массы и материалов коленчатого вала, следовательно, передаточная функция определяется типом коленчатого вала и для ее идентификации необходим специальный эксперимент. Идентификация модели коленчатого вала с трещиной производится в том же порядке.
При анализе свободных колебаний механических систем значение имеют измерения вблизи резонансной частоты. Исходя из того что частотные составляющие вблизи резонансной частоты располагаются близко друг к другу, при составлении математической модели возможно использование общего декремента затухания α.
На основании приведенных формул в среде Mathcad строится амплитудно-частотная характеристика динамической системы коленчатого вала. На основании амплитудно-частотной характеристики можно получить добротность, которая для коленчатого вала с трещиной будет ниже, чем у коленчатого вала без дефекта. Таким
образом, методика определения добротности коленчатого вала на основании анализа его, как динамической системы может быть представлена в виде ряда этапов:
1. Измерение виброакустических колебаний коленчатого вала при импульсном воздействии.
2. Применение к полученному виброакустическому сигналу низкочастотной фильтрации.
3. Аппроксимация полученной импульсной переходной функции при помощи аналитических выражений.
4. Вычисление передаточной функции динамической системы коленчатого вала.
5. Построение амплитудно-частотной характеристики динамической системы коленчатого вала по полученной передаточной функции.
6. Определение добротности системы по полученной амплитудно-частотной характеристике.
7. Сравнение полученной добротности динамической системы коленчатого вала с эталонным бездефектным значением добротности,
8. Отбраковка коленчатого вала в случае выявления в нем дефекта и отправка на утилизацию.
9. В случае соответствия добротности рассматриваемого коленчатого вала нормативным значениям, производится его восстановление.
Таким образом, представленный алгоритм виброакустической дефектовки коленчатого вала позволяет разработать технологию выбраковки со снижением трудоемкости и повышением объективности, что ведет к снижению стоимости ремонта двигателя.