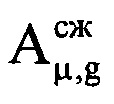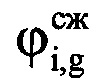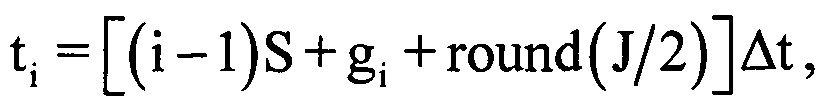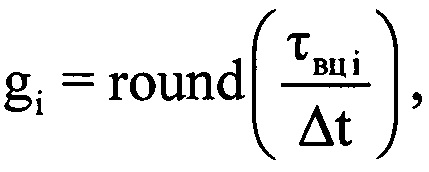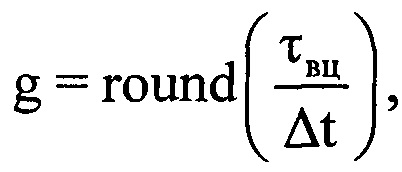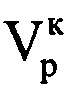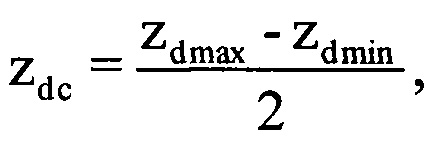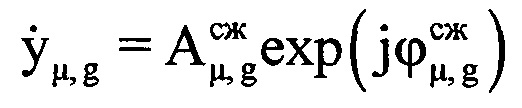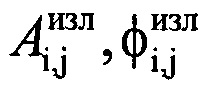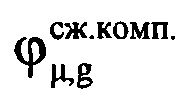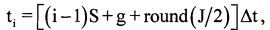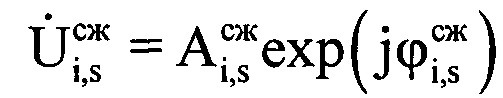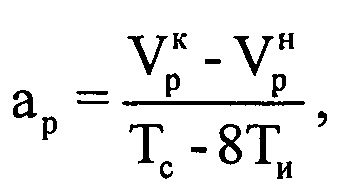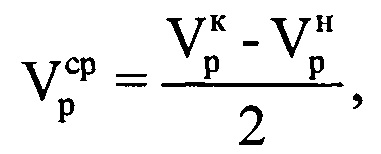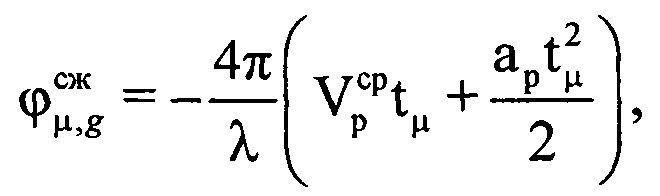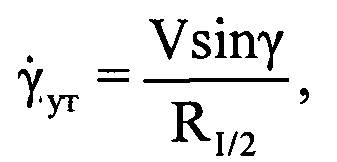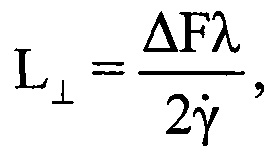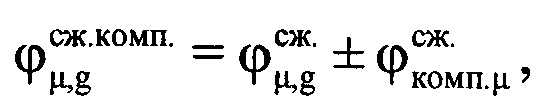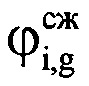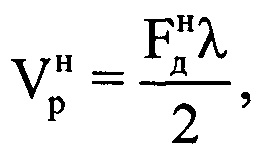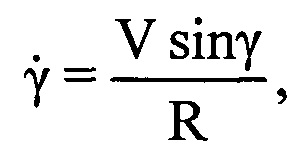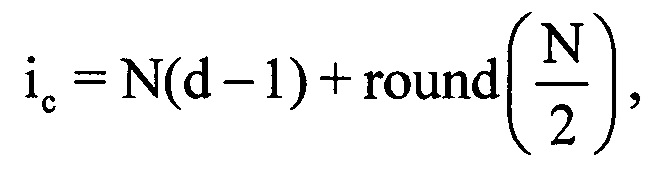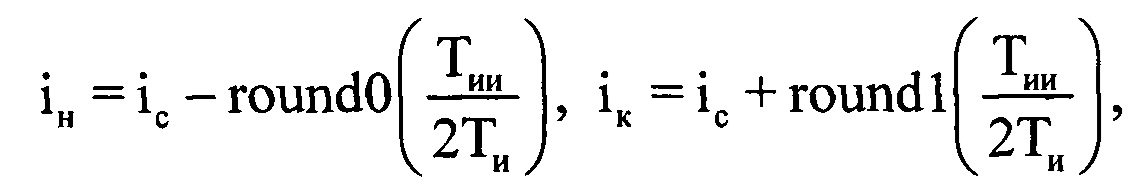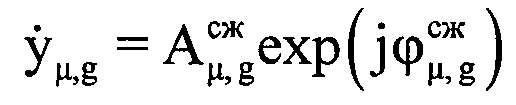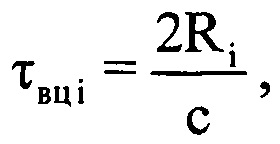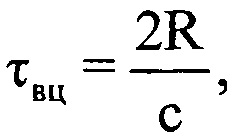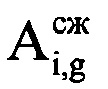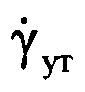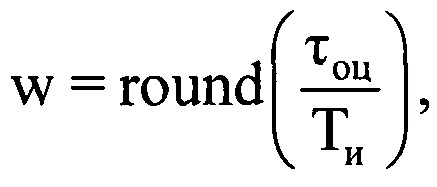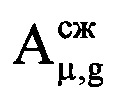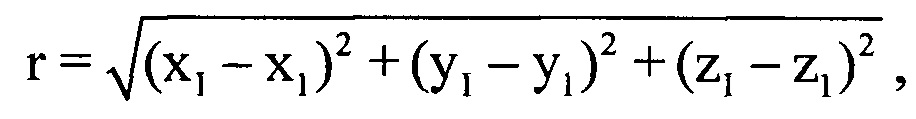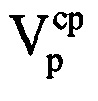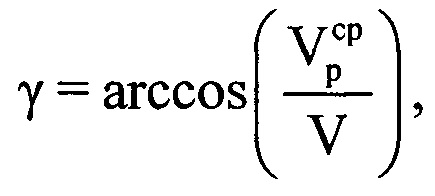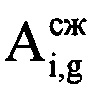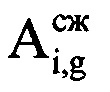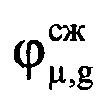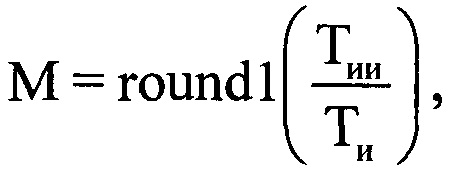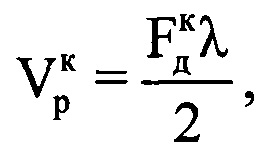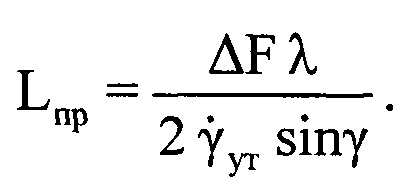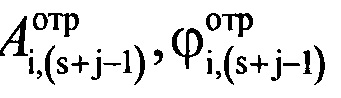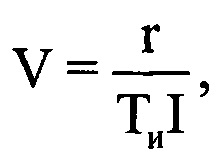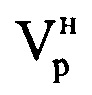Результат интеллектуальной деятельности: Способ оценки пространственного размера воздушной цели по частотной протяженности доплеровского портрета
Вид РИД
Изобретение
Изобретение относится к радиолокационным методам и предназначено для извлечения из доплеровских портретов (ДпП) воздушных целей (ВЦ) признака идентификации в виде пространственного размера ВЦ, оцененного по частотной протяженности ДпП.
В настоящее время использование признаков идентификации ВЦ в виде радиолокационных портретов является общепринятым. Однако используемые методы построения портретов не обеспечивают адекватной оценки размеров или конфигурации ВЦ из-за того, что являются проекциями на поперечное или продольное направление и не учитывают пространственного расположения ВЦ. Вследствие этого идентификацию чаще проводят по простейшим признакам, извлекаемым из структуры ДпП. Одним из таких признаков является размер ВЦ, воспроизводимый протяженностью портрета [1].
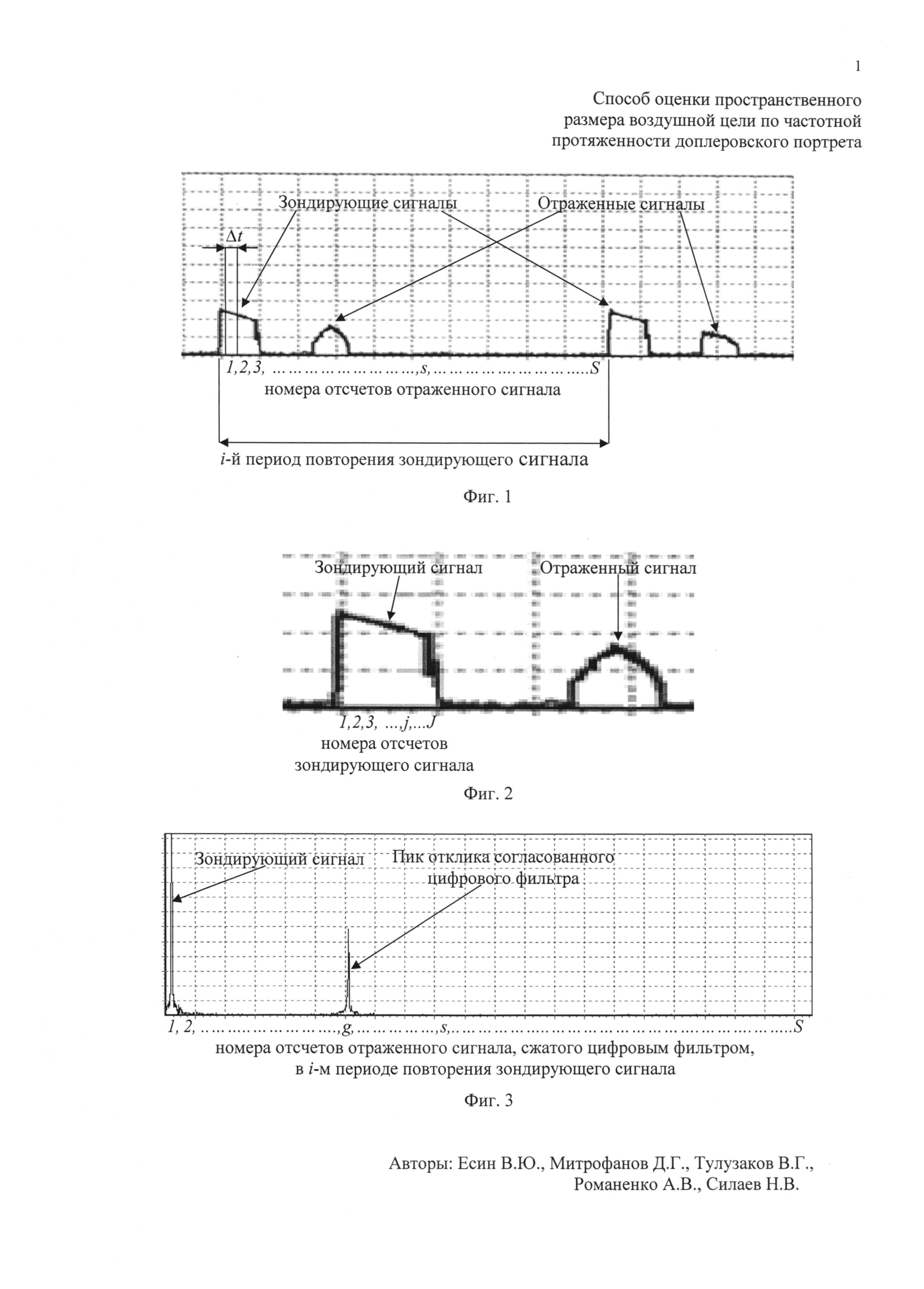
В настоящее время известен способ оценки размера ВЦ по частотной протяженности ДпП, описанный в [2], заключающийся в том, что в направлении реальной ВЦ с помощью радиолокационной станции (РЛС) излучают сверхвысокочастотные импульсные сигналы одинаковой несущей частоты сантиметрового диапазона, последовательно принимают отраженные ВЦ сигналы, переводят РЛС после обнаружения воздушной цели в режим автоматического сопровождения по угловым координатам и дальности. Определяют дальность R до воздушной цели, дискретизируют отраженные от ВЦ сигналы с помощью аналого-цифрового преобразователя (АЦП) с периодом дискретизации Δt, который на порядок меньше длительности импульса τи. Записывают в память электронно-вычислительной машины (ЭВМ) амплитуду Ai,s и фазу ϕi,s каждого s-го отраженного сигнала и просочившегося в приемный тракт излученного сигнала каждого i-го периода повторения Ти. Получают в каждом периоде повторения S дискретных отсчетов (фиг. 1). При этом в пределах длительности зондирующего сигнала (ЗС) для каждого периода повторения будет укладываться J дискретных отсчетов (фиг. 2). Проводят свертку принятых отраженных от ВЦ сигналов каждого i-го периода повторения с оцифрованным комплексно-сопряженным ЗС этого же периода повторения для получения откликов согласованного цифрового фильтра (фиг. 3) по формуле
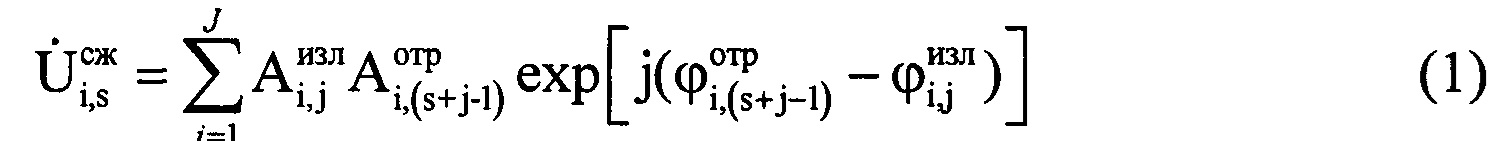
где i=1…I - номер периода повторения РЛС; s=1…(S-J); 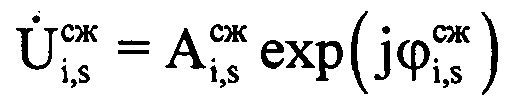 - комплексные значения отражений, получаемые после сжатия отраженного сигнала цифровым фильтром, соответствующие s-му отсчету отраженного сигнала в i-м периоде повторения;
- комплексные значения отражений, получаемые после сжатия отраженного сигнала цифровым фильтром, соответствующие s-му отсчету отраженного сигнала в i-м периоде повторения; 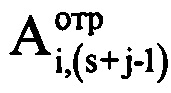 ,
, 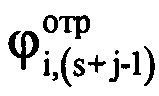 - значения амплитуды и фазы отраженного сигнала, соответствующие (s+j-1)-му отсчету продискретизированного отраженного сигнала в i-м периоде повторения импульсов;
- значения амплитуды и фазы отраженного сигнала, соответствующие (s+j-1)-му отсчету продискретизированного отраженного сигнала в i-м периоде повторения импульсов; 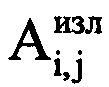 ,
, 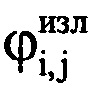 - значения амплитуды и фазы излученного сигнала, соответствующие j-му отсчету продискретизированного ЗС в i-м периоде повторения импульсов; I - количество периодов повторения ЗС, укладывающееся на интервале регистрации данных. Рассчитывают время прохождения излученного сигнала τвц до ВЦ и обратно по формуле
- значения амплитуды и фазы излученного сигнала, соответствующие j-му отсчету продискретизированного ЗС в i-м периоде повторения импульсов; I - количество периодов повторения ЗС, укладывающееся на интервале регистрации данных. Рассчитывают время прохождения излученного сигнала τвц до ВЦ и обратно по формуле 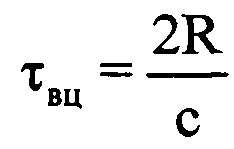 , где с - скорость распространения электромагнитных волн. Определяют предполагаемый номер отсчета g, на который при дальности R будет приходиться пик отраженного от ВЦ сигнала по формуле
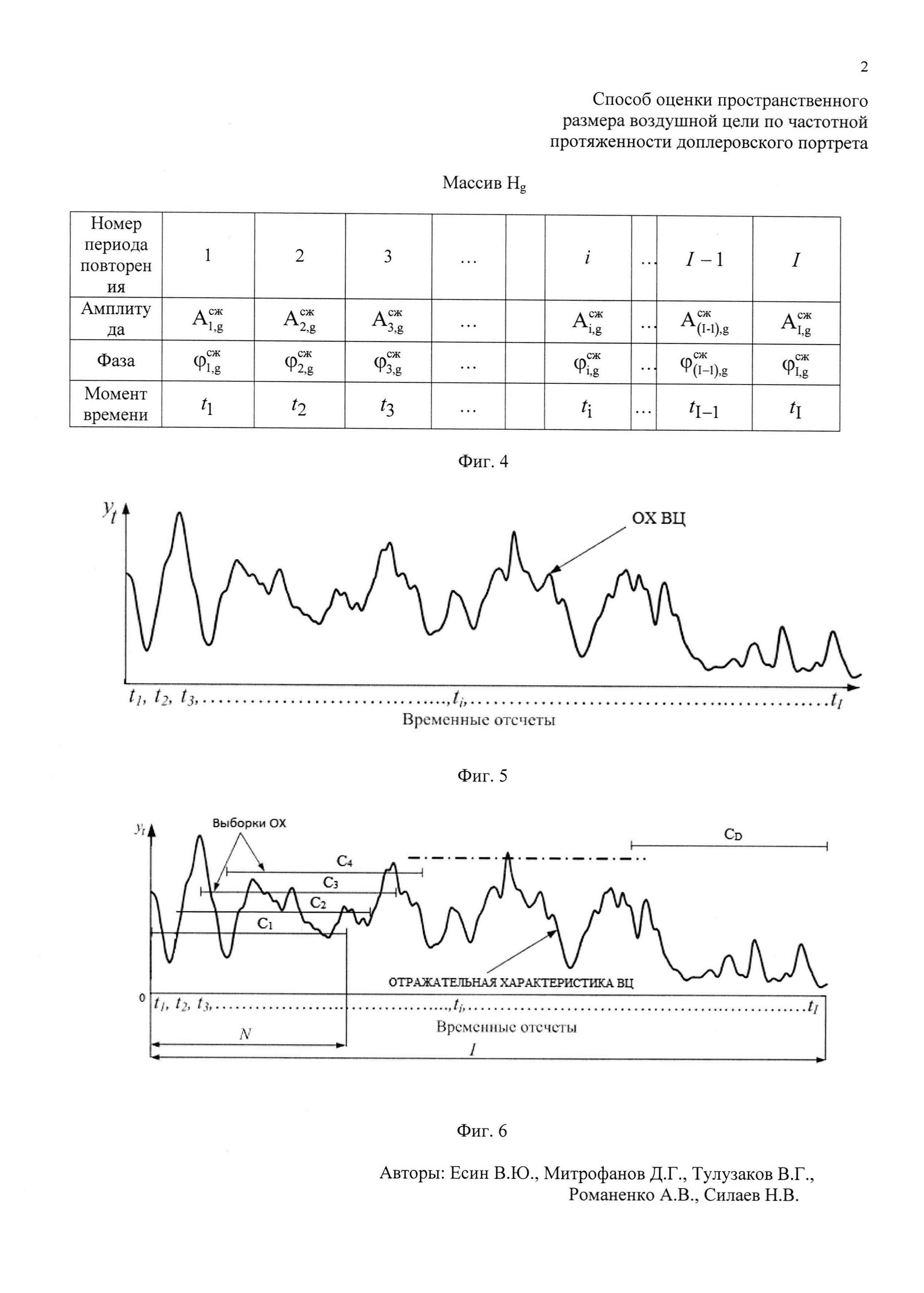
, где с - скорость распространения электромагнитных волн. Определяют предполагаемый номер отсчета g, на который при дальности R будет приходиться пик отраженного от ВЦ сигнала по формуле  , где round(*) - операция округления значения аргумента * до целого числа. В памяти ЭВМ РЛС формируют четырехстрочный массив отражений Hg (фиг. 4), в первую строку которого записывают номера используемых при анализе отражений i-x периодов повторения, во вторую - амплитуды
, где round(*) - операция округления значения аргумента * до целого числа. В памяти ЭВМ РЛС формируют четырехстрочный массив отражений Hg (фиг. 4), в первую строку которого записывают номера используемых при анализе отражений i-x периодов повторения, во вторую - амплитуды 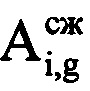 g-x отсчетов сжатого сигнала, которые соответствуют пикам откликов отраженного от воздушной цели сигнала в i-x периодах повторения, в третью - фазы
g-x отсчетов сжатого сигнала, которые соответствуют пикам откликов отраженного от воздушной цели сигнала в i-x периодах повторения, в третью - фазы 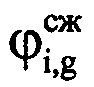 g-x отсчетов сжатого сигнала, которые соответствуют пикам откликов отраженных сигналов в i-x периодах повторения, в четвертую - моменты времени
g-x отсчетов сжатого сигнала, которые соответствуют пикам откликов отраженных сигналов в i-x периодах повторения, в четвертую - моменты времени 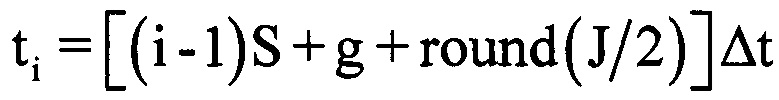 , соответствующие амплитудам
, соответствующие амплитудам 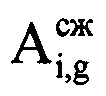 и фазам
и фазам 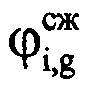 сжатых отраженных от воздушной цели сигналов в i-x периодах повторения. Формируют последовательность из амплитудных значений
сжатых отраженных от воздушной цели сигналов в i-x периодах повторения. Формируют последовательность из амплитудных значений 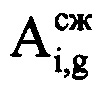 массива Hg, которая графически представляет собой амплитудную отражательную характеристику (ОХ) ВЦ (фиг. 5). Из созданной последовательности, начиная с ее первого отсчета, последовательно извлекают d-e выборки Cd амплитуд отражений, смещенные друг относительно друга на один отсчет амплитудной ОХ, содержащие по N отсчетов (фиг. 6), причем
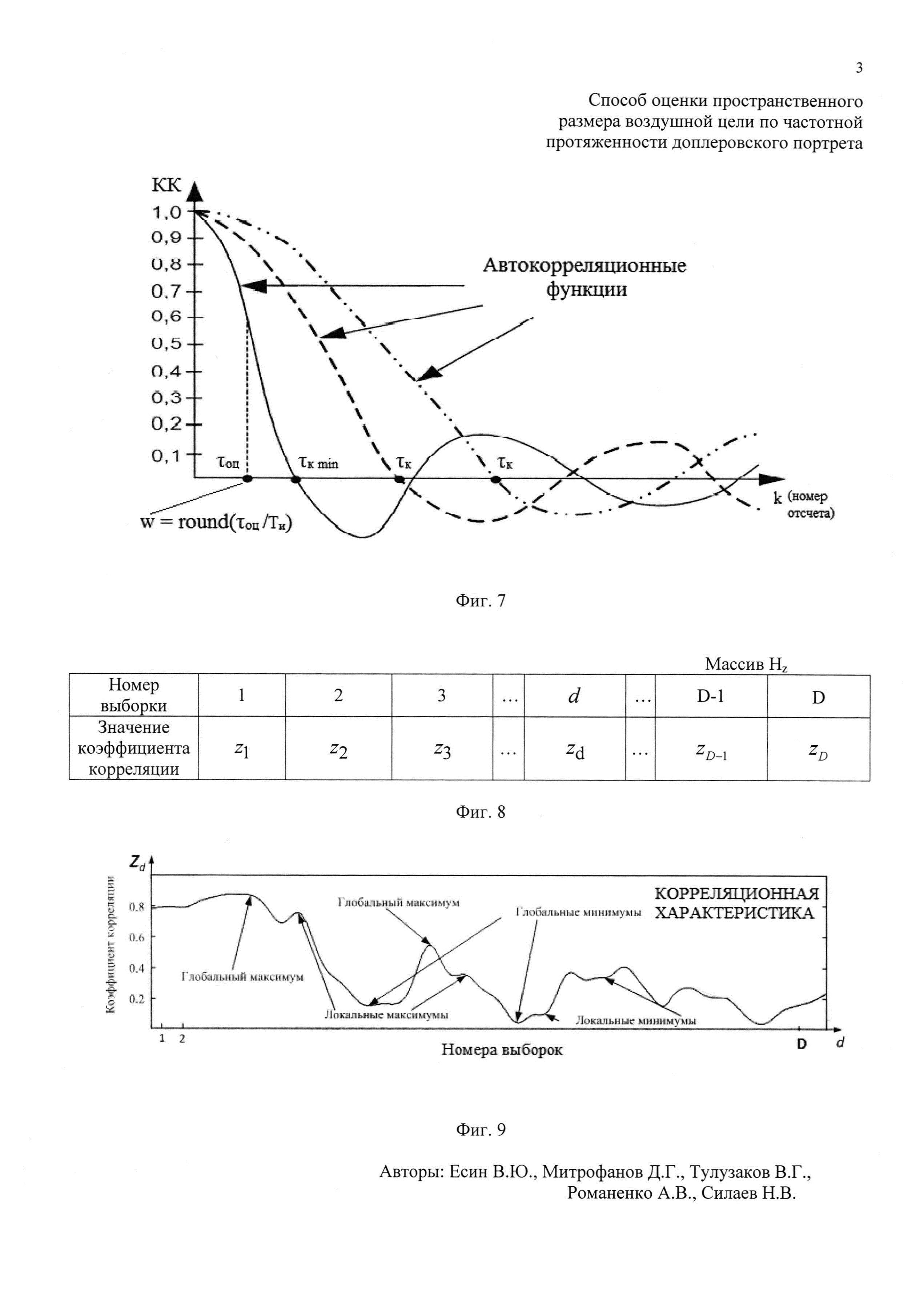
массива Hg, которая графически представляет собой амплитудную отражательную характеристику (ОХ) ВЦ (фиг. 5). Из созданной последовательности, начиная с ее первого отсчета, последовательно извлекают d-e выборки Cd амплитуд отражений, смещенные друг относительно друга на один отсчет амплитудной ОХ, содержащие по N отсчетов (фиг. 6), причем 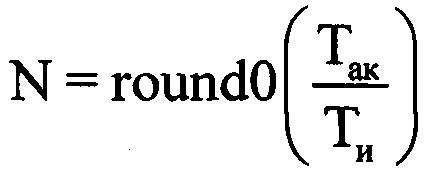 , где round0(*) - операция округления значения аргумента * до ближайшего предшествующего целого числа, Ти - период повторения импульсов, а Так - длительность интервала анализа корреляции, которую выбирают равной 0,5 с. Для каждой полученной выборки Cd формируют автокорреляционную функцию (АКФ) и определяют величину интервала корреляции τк (момент времени, когда АКФ первый раз становится равной нулю). Далее выбирают минимальную среди всех интервалов корреляции τк величину τкmin (фиг. 7). Определяют оценочное время корреляции τоц, равное величине 0,5 τкmin. Для каждой d-й выборки Cd определяют коэффициент корреляции (КК) zd, соответствующий w-му отсчету АКФ, где
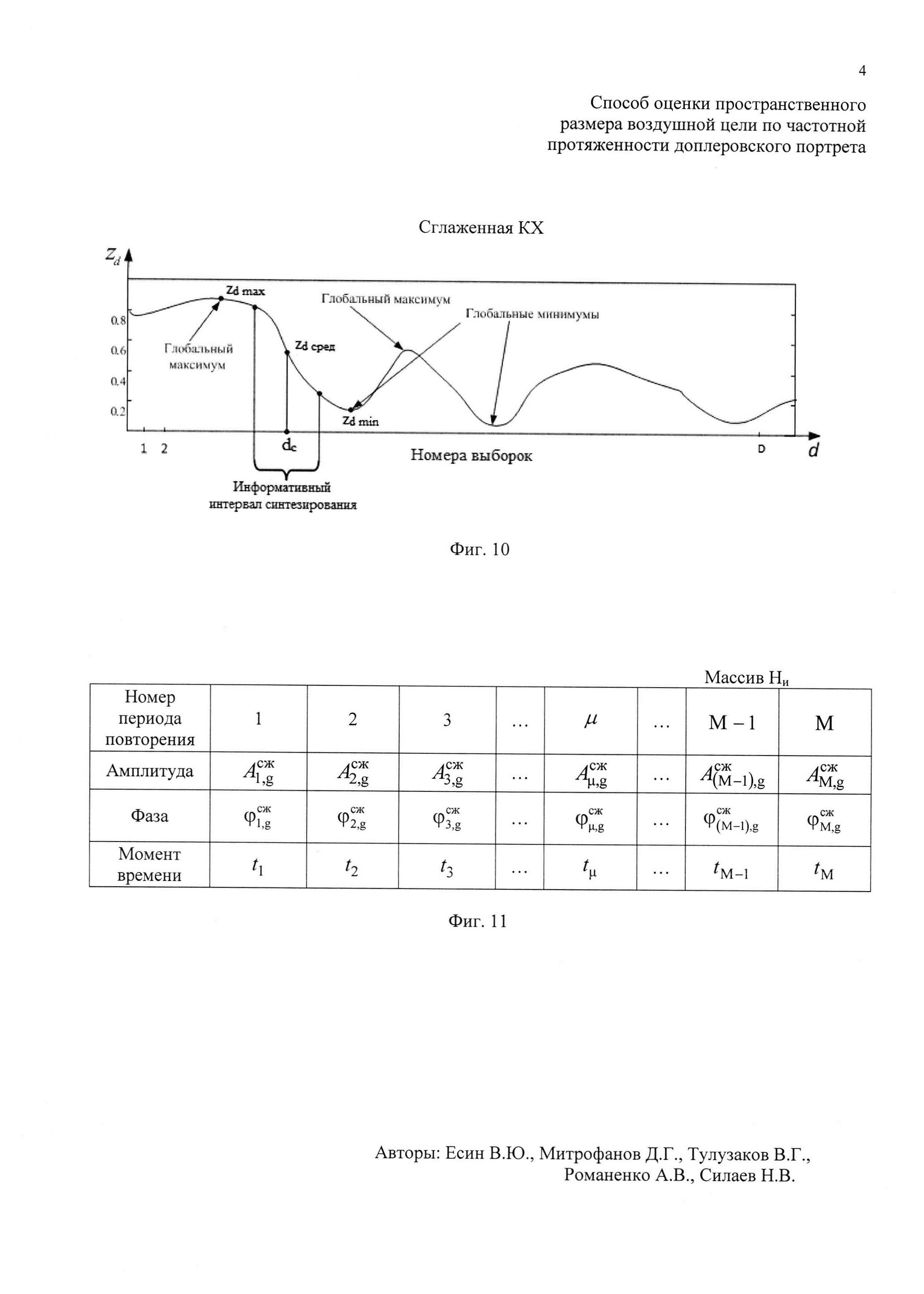
, где round0(*) - операция округления значения аргумента * до ближайшего предшествующего целого числа, Ти - период повторения импульсов, а Так - длительность интервала анализа корреляции, которую выбирают равной 0,5 с. Для каждой полученной выборки Cd формируют автокорреляционную функцию (АКФ) и определяют величину интервала корреляции τк (момент времени, когда АКФ первый раз становится равной нулю). Далее выбирают минимальную среди всех интервалов корреляции τк величину τкmin (фиг. 7). Определяют оценочное время корреляции τоц, равное величине 0,5 τкmin. Для каждой d-й выборки Cd определяют коэффициент корреляции (КК) zd, соответствующий w-му отсчету АКФ, где  . Формируют в памяти ЭВМ РЛС двухстрочный массив Hz, в первую строку которого записывают соответствующие d-e номера АКФ, во вторую - соответствующие им оценочные КК zd (фиг. 8). Из значений КК zd массива Hz формируют последовательность, графически представляющую собой корреляционную характеристику (КХ) отражений ВЦ (фиг. 9). Проводят цифровым способом одним из известных методов, например, методом наименьших квадратов [3], сглаживание сформированной КХ (фиг. 10), то есть устраняют локальные максимумы и минимумы, оставляя только глобальные. Далее определяют в сглаженной КХ такой ее участок между соседними глобальными максимумом zdmax и минимумом zdmin, на котором максимальное zdmax и минимальное zdmin значения коэффициентов корреляции имеют наибольшее отличие (фиг. 10). Находят на этом участке точку КХ со значением КК zd сред, которое наиболее точно соответствует величине
. Формируют в памяти ЭВМ РЛС двухстрочный массив Hz, в первую строку которого записывают соответствующие d-e номера АКФ, во вторую - соответствующие им оценочные КК zd (фиг. 8). Из значений КК zd массива Hz формируют последовательность, графически представляющую собой корреляционную характеристику (КХ) отражений ВЦ (фиг. 9). Проводят цифровым способом одним из известных методов, например, методом наименьших квадратов [3], сглаживание сформированной КХ (фиг. 10), то есть устраняют локальные максимумы и минимумы, оставляя только глобальные. Далее определяют в сглаженной КХ такой ее участок между соседними глобальными максимумом zdmax и минимумом zdmin, на котором максимальное zdmax и минимальное zdmin значения коэффициентов корреляции имеют наибольшее отличие (фиг. 10). Находят на этом участке точку КХ со значением КК zd сред, которое наиболее точно соответствует величине 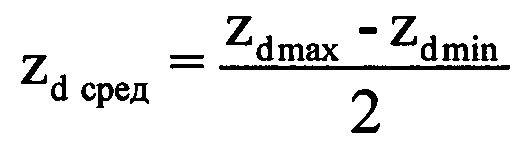 . Используют эту точку как середину информативного интервала синтезирования Тии длительностью Тии=0,5 с. По номеру выборки dc, соответствующему КК zd сред, определяют соответствующую dc-ю выборку ОХ. Далее находят отсчет, соответствующий середине dc-й выборки и определяют его номер в ОХ по формуле
. Используют эту точку как середину информативного интервала синтезирования Тии длительностью Тии=0,5 с. По номеру выборки dc, соответствующему КК zd сред, определяют соответствующую dc-ю выборку ОХ. Далее находят отсчет, соответствующий середине dc-й выборки и определяют его номер в ОХ по формуле 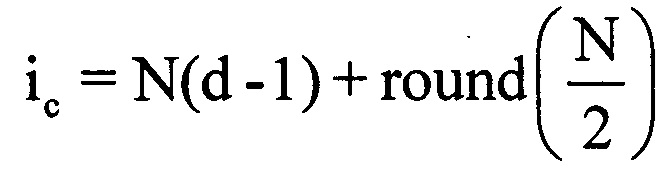 . Принимают длительность Тии за длительность информативного интервала синтезирования Тс. Вычисляют номера отсчетов в ОХ, которые являются началом iн и концом iк информативного интервала синтезирования по соответствующим формулам
. Принимают длительность Тии за длительность информативного интервала синтезирования Тс. Вычисляют номера отсчетов в ОХ, которые являются началом iн и концом iк информативного интервала синтезирования по соответствующим формулам  ,
, 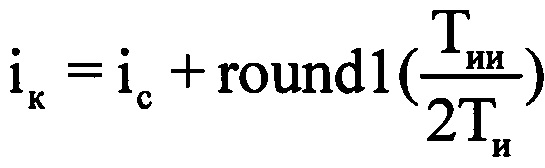 , где round1(*) - операция округления значения аргумента * до ближайшего следующего целого числа. Из массива Hg отражений извлекают амплитудные и фазовые значения, входящие в интервал синтезирования Тс, ограниченные номерами отсчетов слева iн (начальный) и справа iк (конечный). Далее создают в памяти ЭВМ РЛС четырехстрочный массив Ни (фиг. 11), в первую строку которого записывают μ-е номера периодов повторения с 1-го по М-й, причем
, где round1(*) - операция округления значения аргумента * до ближайшего следующего целого числа. Из массива Hg отражений извлекают амплитудные и фазовые значения, входящие в интервал синтезирования Тс, ограниченные номерами отсчетов слева iн (начальный) и справа iк (конечный). Далее создают в памяти ЭВМ РЛС четырехстрочный массив Ни (фиг. 11), в первую строку которого записывают μ-е номера периодов повторения с 1-го по М-й, причем  , а μ-й номер в пределах массива Ни соответствует (iн+μ-1)-му номеру в исходной ОХ, во вторую - амплитуды
, а μ-й номер в пределах массива Ни соответствует (iн+μ-1)-му номеру в исходной ОХ, во вторую - амплитуды 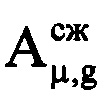 μ-х отсчетов участка ОХ, входящего в информативный интервал синтезирования, в третью - фазы
μ-х отсчетов участка ОХ, входящего в информативный интервал синтезирования, в третью - фазы 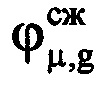 соответствующих μ-х отсчетов ОХ, принадлежащих информативному интервалу, в четвертую - моменты времени tμ=(iн+μ-1)Ти, соответствующие амплитудам и фазам отраженных сигналов в μ-х периодах повторения. При этом первый элемент массива Ни соответствует началу интервала синтезирования, то есть iн-му элементу массива Hg, а последний элемент массива Ни соответствует концу интервала синтезирования, то есть iк-му элементу массива Hg. Далее проводят операцию быстрого дискретного преобразования Фурье с комплексными значениями
соответствующих μ-х отсчетов ОХ, принадлежащих информативному интервалу, в четвертую - моменты времени tμ=(iн+μ-1)Ти, соответствующие амплитудам и фазам отраженных сигналов в μ-х периодах повторения. При этом первый элемент массива Ни соответствует началу интервала синтезирования, то есть iн-му элементу массива Hg, а последний элемент массива Ни соответствует концу интервала синтезирования, то есть iк-му элементу массива Hg. Далее проводят операцию быстрого дискретного преобразования Фурье с комплексными значениями 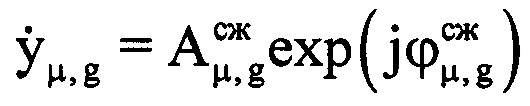 выборки, состоящей из 8-ми первых отсчетов массива Ни, в результате преобразования получают начальный низкоинформативный доплеровский спектр. Определяют в полученном начальном низкоинформативном доплеровском спектре частоту Доплера
выборки, состоящей из 8-ми первых отсчетов массива Ни, в результате преобразования получают начальный низкоинформативный доплеровский спектр. Определяют в полученном начальном низкоинформативном доплеровском спектре частоту Доплера 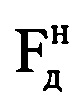 , которая соответствует максимальной по амплитуде составляющей спектра. Определяют радиальную скорость ВЦ в начале информативного интервала синтезирования
, которая соответствует максимальной по амплитуде составляющей спектра. Определяют радиальную скорость ВЦ в начале информативного интервала синтезирования  по формуле
по формуле 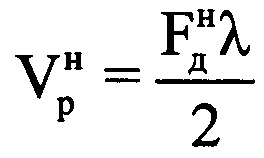 , где λ - длина волны излученного сигнала. Проводят операцию быстрого дискретного преобразования Фурье с комплексными значениями выборки, состоящей из 8-ми последних отсчетов массива Ни, в результате которого получают конечный низкоинформативный доплеровский спектр. После этого определяют в полученном конечном низкоинформативном доплеровском спектре частоту Доплера
, где λ - длина волны излученного сигнала. Проводят операцию быстрого дискретного преобразования Фурье с комплексными значениями выборки, состоящей из 8-ми последних отсчетов массива Ни, в результате которого получают конечный низкоинформативный доплеровский спектр. После этого определяют в полученном конечном низкоинформативном доплеровском спектре частоту Доплера 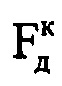 , которая соответствует максимальной по амплитуде составляющей спектра. Определяют радиальную скорость ВЦ в конце интервала синтезирования
, которая соответствует максимальной по амплитуде составляющей спектра. Определяют радиальную скорость ВЦ в конце интервала синтезирования 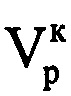 по формуле
по формуле 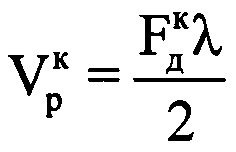 . Определяют среднюю радиальную скорость
. Определяют среднюю радиальную скорость 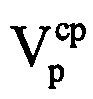 воздушной цели в пределах интервала синтезирования по формуле
воздушной цели в пределах интервала синтезирования по формуле 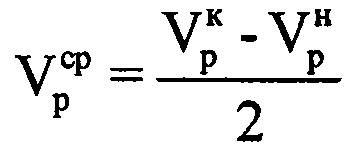 . Далее определяют радиальное ускорение ар воздушной цели на выбранном информативном интервале синтезирования по формуле
. Далее определяют радиальное ускорение ар воздушной цели на выбранном информативном интервале синтезирования по формуле 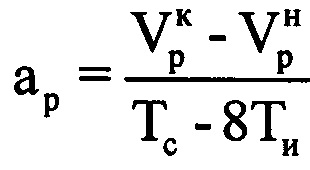 . Рассчитывают на основе полученных значений средней радиальной скорости
. Рассчитывают на основе полученных значений средней радиальной скорости 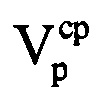 и ускорения ар величину компенсируемой фазы для каждого tμ-го момента времени, входящего в информативный интервал синтезирования по формуле
и ускорения ар величину компенсируемой фазы для каждого tμ-го момента времени, входящего в информативный интервал синтезирования по формуле 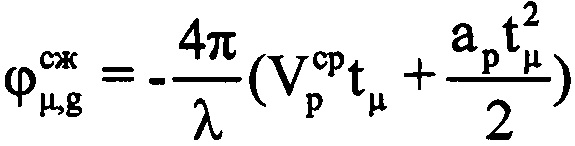 . Проводят компенсацию фазового влияния радиального движения воздушной цели на информативном интервале синтезирования путем изменения фазы по формуле
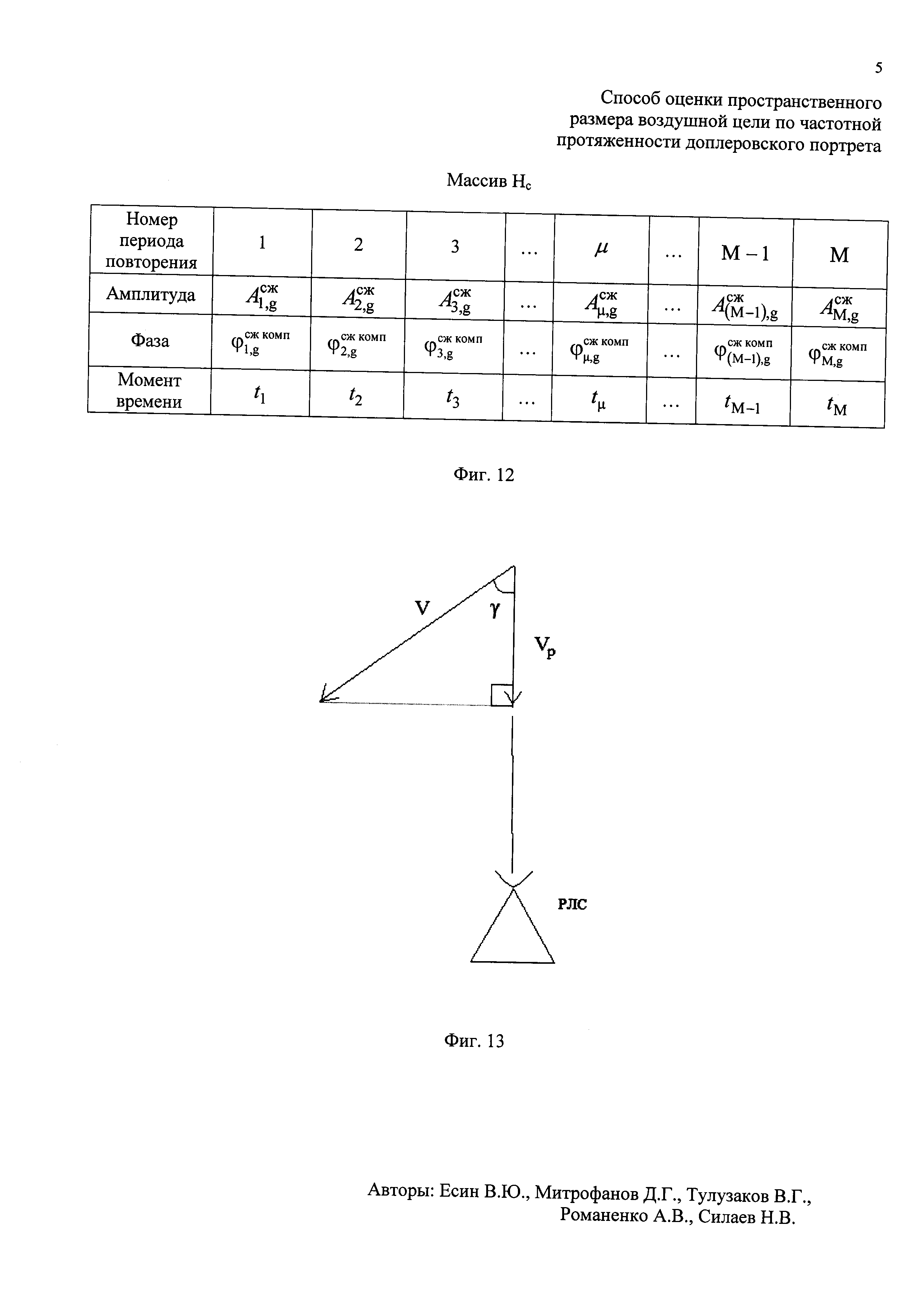
. Проводят компенсацию фазового влияния радиального движения воздушной цели на информативном интервале синтезирования путем изменения фазы по формуле 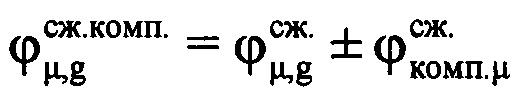 , где знак «-» соответствует движению воздушной цели в направлении радиолокационной станции, т.е. приближению, а знак «+» соответствует удалению ВЦ. Создают в памяти ЭВМ РЛС четырехстрочный массив Нс (фиг. 12), в первую строку которого записывают номера периодов повторения с 1-го по М-й, во вторую - амплитуды
, где знак «-» соответствует движению воздушной цели в направлении радиолокационной станции, т.е. приближению, а знак «+» соответствует удалению ВЦ. Создают в памяти ЭВМ РЛС четырехстрочный массив Нс (фиг. 12), в первую строку которого записывают номера периодов повторения с 1-го по М-й, во вторую - амплитуды 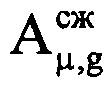 μ-x отсчетов ОХ, принадлежащих информативному интервалу синтезирования, в третью - скомпенсированные фазы
μ-x отсчетов ОХ, принадлежащих информативному интервалу синтезирования, в третью - скомпенсированные фазы 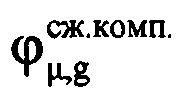 μ-х отсчетов ОХ, принадлежащих информативному интервалу синтезирования, в четвертую - моменты времени tμ, соответствующие амплитудам и фазам отраженных сигналов в μ-x периодах повторения. Для осуществления быстрого дискретного преобразования Фурье полученный массив дискретных отсчетов расширяют путем ввода новых элементов с нулевыми значениями амплитуд и фаз, добиваясь числа элементов массива Нс, равного Е=2m, где Е - ближайшее целое число, удовлетворяющее условию Е=2m и Е>М, m - целое число, например, m=8, m=9 и т.п. Проводят операцию быстрого дискретного преобразования Фурье с вектором комплексных величин
μ-х отсчетов ОХ, принадлежащих информативному интервалу синтезирования, в четвертую - моменты времени tμ, соответствующие амплитудам и фазам отраженных сигналов в μ-x периодах повторения. Для осуществления быстрого дискретного преобразования Фурье полученный массив дискретных отсчетов расширяют путем ввода новых элементов с нулевыми значениями амплитуд и фаз, добиваясь числа элементов массива Нс, равного Е=2m, где Е - ближайшее целое число, удовлетворяющее условию Е=2m и Е>М, m - целое число, например, m=8, m=9 и т.п. Проводят операцию быстрого дискретного преобразования Фурье с вектором комплексных величин 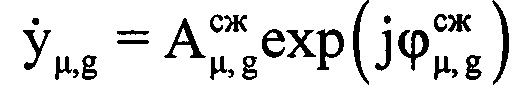 из массива Нс [3, 4]. Получают массив Ндоп, содержащий Е комплексных значений спектра отраженного сигнала, который представляет собой доплеровский портрет ВЦ [5-12], полученный на информативном интервале синтезирования Тс [2, 13-15]. В полученном массиве Ндоп, характеризующем доплеровский портрет, определяют крайний левый и крайний правый максимумы путем перебора и анализа амплитудных значений элементов массива Ндоп. Далее записывают в память ЭВМ РЛС номера отсчетов iн макс и iк макс в массиве Ндоп, соответствующих начальному и конечному максимумам. Вычисляют частотную протяженностью ΔF доплеровского портрета ВЦ по формуле ΔF=(iк макс-iн макс)/Тс. Предполагают, что все ВЦ движутся с близкими по величине курсовыми углами γ и заранее известной путевой скоростью V. Рассчитывают угловую скорость поворота ВЦ относительно РЛС по формуле
из массива Нс [3, 4]. Получают массив Ндоп, содержащий Е комплексных значений спектра отраженного сигнала, который представляет собой доплеровский портрет ВЦ [5-12], полученный на информативном интервале синтезирования Тс [2, 13-15]. В полученном массиве Ндоп, характеризующем доплеровский портрет, определяют крайний левый и крайний правый максимумы путем перебора и анализа амплитудных значений элементов массива Ндоп. Далее записывают в память ЭВМ РЛС номера отсчетов iн макс и iк макс в массиве Ндоп, соответствующих начальному и конечному максимумам. Вычисляют частотную протяженностью ΔF доплеровского портрета ВЦ по формуле ΔF=(iк макс-iн макс)/Тс. Предполагают, что все ВЦ движутся с близкими по величине курсовыми углами γ и заранее известной путевой скоростью V. Рассчитывают угловую скорость поворота ВЦ относительно РЛС по формуле 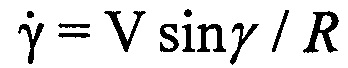 . На конечном этапе находят поперечный размер ВЦ по формуле
. На конечном этапе находят поперечный размер ВЦ по формуле  и принимают его за пространственный размер ВЦ.
и принимают его за пространственный размер ВЦ.
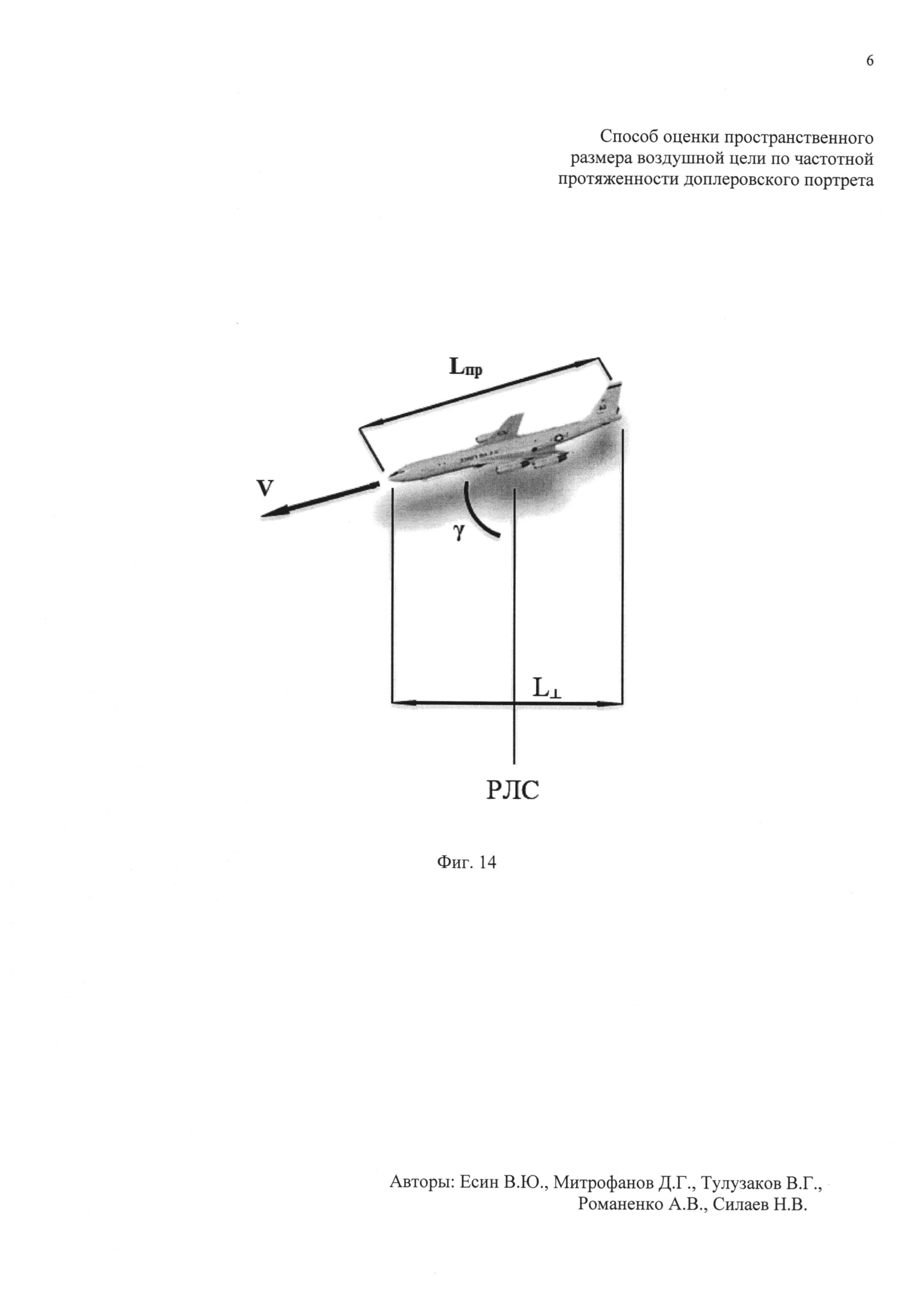
Описанный способ не может быть признан эффективным вследствие того, что ряд параметров, используемых при определении размера ВЦ оцениваются недостаточно точно, а именно, при оценке размера ВЦ способом [2] предполагают, что все цели движутся с близкими по величине курсовыми углами γ и заранее известной путевой скоростью V, что выполняется не всегда, а точнее - почти никогда не выполняется. К тому же способ [2] приводит к измерению длины проекции L⊥ силуэта (размера) ВЦ на поперечное относительно линии визирования направление [16], что не позволяет сравнивать ВЦ между собой, так как проекция крупной цели с меньшим ракурсом полета может быть равна проекции малой цели с большим ракурсом (с боковым ракурсом, с большой величиной курсового угла). Соответствующий протяженности сформированного ДпП размер ВЦ находится в зависимости от величины курсового угла ВЦ γ, что способом не учитывается. И наконец, дальность R до ВЦ в описанном выше способе [2] измеряется только в момент начала регистрации данных, а за время регистрации дальность до ВЦ меняется, вследствие чего ОХ, используемая для построения ДпП, формируется с искажениями, и результирующий ДпП имеет неточности в своей внутренней структуре.
Задачей изобретения является устранение неточностей, присущих известному способу оценки размера ВЦ по протяженности ДпП, т.е. совершенствование способа оценки размера ВЦ по протяженности ДпП путем учета дополнительных параметров, таких как координаты ВЦ, путевая скорость ВЦ, угловая скорость поворота относительно радиолокационной станции (РЛС), текущая (изменяемая во времени) дальность и др.
Для решения задачи изобретения предлагается дополнительно учесть ряд факторов. Например, предлагается учесть, что за время регистрации данных дальность до ВЦ меняется. В прототипе считалось, что при расчетах и преобразованиях можно ограничиться начальной дальностью. Между тем дальность до ВЦ не является постоянной, а значит ОХ, получаемая из отсчетов с номером g в каждом периоде повторения, не будет соответствовать во всех периодах повторения пикам отклика отраженного сигнала. Соответственно и ДпП ВЦ, полученный из фрагмента ОХ, получит искажения, ведущие к нарушению структуры ДпП. Расчет угловой скорости поворота ВЦ также ориентирован на использование начальной дальности до цели, что не совсем корректно. В новом способе при расчете угловой скорости поворота ВЦ предлагается использовать дальность, соответствующую серединному отсчету на интервале регистрации. Для этого предлагается измерять дальность в каждом периоде повторения и фиксировать ее значение с помощью АЦП. Также в способе [2] предполагают, что все ВЦ движутся с близкими по величине курсовыми углами γ и заранее известной путевой скоростью V, что в реальной обстановке не выполняется. Поэтому в новом способе предлагается по изменению координат ВЦ оценивать (рассчитывать) путь, проделанный целью, и определять путевую скорость полета. В способе [2] подразумевают проводить оценку поперечного размера ВЦ, который является проекцией пространственного размера ВЦ на поперечное относительно линии визирования направление. Соответствующий ширине сформированного ДпП поперечный размер ВЦ находится в зависимости от величины курсового угла ВЦ [17], что снижает информативность данного признака. Для получения пространственного размера ВЦ по частотной протяженности ДпП в новом способе предлагается учитывать реальный ракурс локации ВЦ, который можно рассчитать по соотношению радиальной и путевой скоростей полета ВЦ [].
Предлагаемый подход приводит к независимости измеряемого размера ВЦ от ракурса локации, что обеспечивает адекватность производимого измерения. Признак размера ВЦ, оцененного предлагаемым способом, может повысить результативность классификации объектов и информативность радиолокационной системы в целом.
В соответствии с изложенной выше идеей, предлагаемый способ оценки пространственного размера ВЦ по частотной протяженности доплеровского портрета заключается в том, что в направлении реальной ВЦ с помощью РЛС излучают сверхвысокочастотные импульсные сигналы одинаковой несущей частоты сантиметрового диапазона, последовательно принимают отраженные от ВЦ сигналы, переводят РЛС после обнаружения ВЦ в режим автоматического сопровождения по угловым координатам и дальности. Из сигналов канала угловой автоматики, пропорциональных углу места ε и азимуту β воздушной цели, с помощью соответствующих аналого-цифровых преобразователей в каждом i-м периоде повторения получают цифровые отсчеты угла места εi и азимута βi. Определяют дальность до ВЦ Ri в каждом i-м периоде повторения. Дискретизируют отраженные ВЦ сигналы с помощью АЦП с периодом дискретизации Δt, который на порядок меньше длительности импульса τи. Записывают в память ЭВМ амплитуду Ai,s и фазу ϕi,s каждого s-го отраженного сигнала и просочившегося в приемный тракт излученного сигнала каждого i-го периода повторения Ти. Получают в каждом периоде повторения S дискретных отсчетов (фиг. 1). При этом в пределах длительности ЗС для каждого периода повторения будет укладываться J дискретных отсчетов (фиг. 2). Проводят свертку принятых отраженных от ВЦ сигналов каждого i-го периода повторения с оцифрованным комплексно-сопряженным ЗС этого же периода повторения для получения откликов согласованного цифрового фильтра (фиг. 3) по формуле
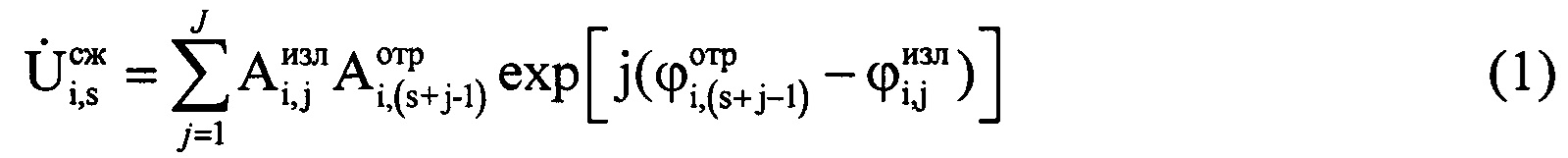
где i=1…I - номер периода повторения РЛС; s=1…(S-J); 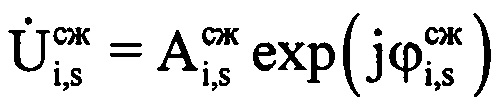 - комплексные значения отражений, получаемые после сжатия отраженного сигнала цифровым фильтром, соответствующие s-му отсчету отраженного сигнала в i-м периоде повторения;
- комплексные значения отражений, получаемые после сжатия отраженного сигнала цифровым фильтром, соответствующие s-му отсчету отраженного сигнала в i-м периоде повторения; 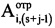 ,
, 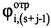 - значения амплитуды и фазы отраженного сигнала, соответствующие (s+j-1)-му отсчету продискретизированного отраженного сигнала в i-м периоде повторения импульсов;
- значения амплитуды и фазы отраженного сигнала, соответствующие (s+j-1)-му отсчету продискретизированного отраженного сигнала в i-м периоде повторения импульсов; 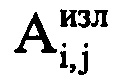 ,
, 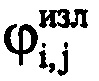 - значения амплитуды и фазы излученного сигнала, соответствующие j-му отсчету продискретизированного ЗС в i-м периоде повторения импульсов; I - количество периодов повторения ЗС, укладывающееся на интервале регистрации данных. Для каждого периода повторения Ти рассчитывают время прохождения излученного сигнала до ВЦ и обратно по формуле
- значения амплитуды и фазы излученного сигнала, соответствующие j-му отсчету продискретизированного ЗС в i-м периоде повторения импульсов; I - количество периодов повторения ЗС, укладывающееся на интервале регистрации данных. Для каждого периода повторения Ти рассчитывают время прохождения излученного сигнала до ВЦ и обратно по формуле 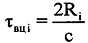 , где с - скорость распространения электромагнитных волн, на основании чего для каждого i-го периода повторения определяют номер отсчета gi оцифрованного отраженного сигнала, на который при дальности до ВЦ Ri будет приходится пик отклика отраженного сигнала после согласованной фильтрации. Для этого используют формулу
, где с - скорость распространения электромагнитных волн, на основании чего для каждого i-го периода повторения определяют номер отсчета gi оцифрованного отраженного сигнала, на который при дальности до ВЦ Ri будет приходится пик отклика отраженного сигнала после согласованной фильтрации. Для этого используют формулу  . Используют значение gi для расчета времени приема отраженного от воздушной цели сигнала в i-м периоде повторения по формуле ti=[(i-1)S+gi+round(J/2)]Δt. В памяти ЭВМ РЛС формируют четырехстрочный массив отражений Hg (фиг. 4), в первую строку которого записывают номера используемых при анализе отражений i-x периодов повторения, во вторую - амплитуды
. Используют значение gi для расчета времени приема отраженного от воздушной цели сигнала в i-м периоде повторения по формуле ti=[(i-1)S+gi+round(J/2)]Δt. В памяти ЭВМ РЛС формируют четырехстрочный массив отражений Hg (фиг. 4), в первую строку которого записывают номера используемых при анализе отражений i-x периодов повторения, во вторую - амплитуды 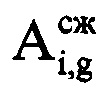 gi-х отсчетов сжатого сигнала, которые соответствуют пикам откликов отраженного от воздушной цели сигнала в i-x периодах повторения на дальности Ri, в третью - фазы
gi-х отсчетов сжатого сигнала, которые соответствуют пикам откликов отраженного от воздушной цели сигнала в i-x периодах повторения на дальности Ri, в третью - фазы 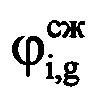 g-x отсчетов сжатого сигнала, которые соответствуют пикам откликов отраженных сигналов в i-x периодах повторения, в четвертую - моменты времени ti=[(i-1)S+gi+round(J/2)]Δt, соответствующие амплитудам
g-x отсчетов сжатого сигнала, которые соответствуют пикам откликов отраженных сигналов в i-x периодах повторения, в четвертую - моменты времени ti=[(i-1)S+gi+round(J/2)]Δt, соответствующие амплитудам 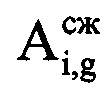 и фазам
и фазам 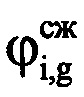 сжатых отраженных от воздушной цели сигналов в i-x периодах повторения. Формируют последовательность из амплитудных значений
сжатых отраженных от воздушной цели сигналов в i-x периодах повторения. Формируют последовательность из амплитудных значений 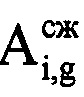 массива Hg, которая графически представляет собой амплитудную ОХ ВЦ (фиг. 5). Из созданной последовательности, начиная с первого отсчета, последовательно извлекают d-e выборки Cd амплитуд отражений, смещенные друг относительно друга на один отсчет амплитудной ОХ, содержащие по N отсчетов (фиг. 6), причем
массива Hg, которая графически представляет собой амплитудную ОХ ВЦ (фиг. 5). Из созданной последовательности, начиная с первого отсчета, последовательно извлекают d-e выборки Cd амплитуд отражений, смещенные друг относительно друга на один отсчет амплитудной ОХ, содержащие по N отсчетов (фиг. 6), причем  , где round0(*) - операция округления значения аргумента * до ближайшего предшествующего целого числа, Ти - период повторения импульсов, а Так - длительность интервала анализа корреляции, равная Так=0,5 с. Для каждой полученной выборки Cd формируют АКФ и определяют величину интервала корреляции τк (момент времени, когда АКФ первый раз становится равной нулю). Далее выбирают минимальную среди всех интервалов корреляции τк величину τкmin (фиг. 7). Определяют оценочное время корреляции τоц, равное величине 0,5 τкmin. Для каждой d-й выборки Cd определяют КК zd, соответствующий w-му отсчету АКФ. Формируют в памяти ЭВМ РЛС двухстрочный массив Hz, в первую строку которого записывают соответствующие d-e номера АКФ, во вторую - соответствующие им оценочные КК zd (фиг. 8). Из значений КК zd формируют последовательность массива Hz, графически представляющую собой КХ отражений ВЦ (фиг. 9). Проводят цифровым способом одним из известных методов, например методом наименьших квадратов [3] сглаживание сформированной КХ (фиг. 10), то есть устраняют локальные максимумы и минимумы, оставляя только глобальные. Далее определяют в сглаженной КХ такой ее участок между соседними глобальными максимумом zdmax и минимумом zdmin, на котором максимальное zdmax и минимальное zdmin значения коэффициентов корреляции имеют наибольшее отличие. Находят на этом участке точку КХ со значением КК zd сред, которое наиболее точно соответствует величине
, где round0(*) - операция округления значения аргумента * до ближайшего предшествующего целого числа, Ти - период повторения импульсов, а Так - длительность интервала анализа корреляции, равная Так=0,5 с. Для каждой полученной выборки Cd формируют АКФ и определяют величину интервала корреляции τк (момент времени, когда АКФ первый раз становится равной нулю). Далее выбирают минимальную среди всех интервалов корреляции τк величину τкmin (фиг. 7). Определяют оценочное время корреляции τоц, равное величине 0,5 τкmin. Для каждой d-й выборки Cd определяют КК zd, соответствующий w-му отсчету АКФ. Формируют в памяти ЭВМ РЛС двухстрочный массив Hz, в первую строку которого записывают соответствующие d-e номера АКФ, во вторую - соответствующие им оценочные КК zd (фиг. 8). Из значений КК zd формируют последовательность массива Hz, графически представляющую собой КХ отражений ВЦ (фиг. 9). Проводят цифровым способом одним из известных методов, например методом наименьших квадратов [3] сглаживание сформированной КХ (фиг. 10), то есть устраняют локальные максимумы и минимумы, оставляя только глобальные. Далее определяют в сглаженной КХ такой ее участок между соседними глобальными максимумом zdmax и минимумом zdmin, на котором максимальное zdmax и минимальное zdmin значения коэффициентов корреляции имеют наибольшее отличие. Находят на этом участке точку КХ со значением КК zd сред, которое наиболее точно соответствует величине 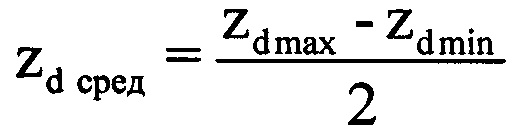 (фиг. 10). Используют эту точку как середину информативного интервала синтезирования длительностью Тии=0,5 с. По номеру выборки dc, соответствующей КК zd сред, определяют соответствующую dc-ю выборку ОХ. Далее находят отсчет, соответствующий середине dc-й выборки и определяют его номер в ОХ по формуле
(фиг. 10). Используют эту точку как середину информативного интервала синтезирования длительностью Тии=0,5 с. По номеру выборки dc, соответствующей КК zd сред, определяют соответствующую dc-ю выборку ОХ. Далее находят отсчет, соответствующий середине dc-й выборки и определяют его номер в ОХ по формуле 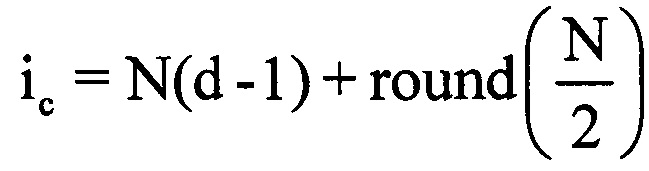 . Принимают длительность Тии за длительность информативного интервала синтезирования Тс. Вычисляют номера отсчетов в ОХ, которые являются началом iн и концом iк информативного интервала синтезирования по соответствующим формулам
. Принимают длительность Тии за длительность информативного интервала синтезирования Тс. Вычисляют номера отсчетов в ОХ, которые являются началом iн и концом iк информативного интервала синтезирования по соответствующим формулам 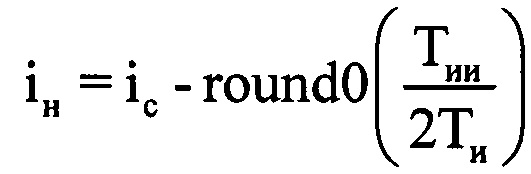 ,
, 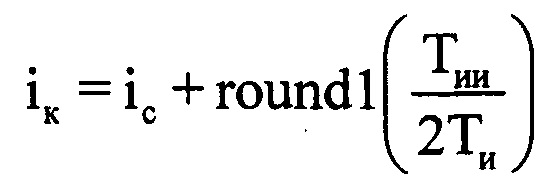 . Из массива Hg отражений извлекают амплитудные и фазовые значения, входящие в информативный интервал синтезирования Тс, ограниченные номерами отсчета слева iн (начальный) и справа iк (конечный). Далее создают в памяти ЭВМ РЛС четырехстрочный массив Ни (фиг. 11), в первую строку которого записывают μ-е номера периодов повторения с 1-го по М-й, причем
. Из массива Hg отражений извлекают амплитудные и фазовые значения, входящие в информативный интервал синтезирования Тс, ограниченные номерами отсчета слева iн (начальный) и справа iк (конечный). Далее создают в памяти ЭВМ РЛС четырехстрочный массив Ни (фиг. 11), в первую строку которого записывают μ-е номера периодов повторения с 1-го по М-й, причем  , а μ-й номер в пределах массива Ни соответствует (iн+μ-1)-му номеру в исходной ОХ, во вторую - амплитуды
, а μ-й номер в пределах массива Ни соответствует (iн+μ-1)-му номеру в исходной ОХ, во вторую - амплитуды 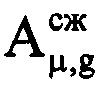 μ-x отсчетов участка ОХ, входящего в информативный интервал синтезирования, в третью - фазы
μ-x отсчетов участка ОХ, входящего в информативный интервал синтезирования, в третью - фазы 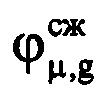 соответствующих μ-х отсчетов ОХ, принадлежащих информативному интервалу синтезирования, в четвертую - моменты времени tμ=(iн+μ-1)Ти, соответствующие амплитудам и фазам отраженных сигналов в μ-х периодах повторения. При этом первый элемент массива Ни соответствует началу информативного интервала синтезирования, то есть iн-му элементу массива Hg, а последний элемент массива Ни соответствует концу информативного интервала синтезирования, то есть iк-му элементу массива Hg. Далее проводят операцию быстрого дискретного преобразования Фурье с комплексными значениями
соответствующих μ-х отсчетов ОХ, принадлежащих информативному интервалу синтезирования, в четвертую - моменты времени tμ=(iн+μ-1)Ти, соответствующие амплитудам и фазам отраженных сигналов в μ-х периодах повторения. При этом первый элемент массива Ни соответствует началу информативного интервала синтезирования, то есть iн-му элементу массива Hg, а последний элемент массива Ни соответствует концу информативного интервала синтезирования, то есть iк-му элементу массива Hg. Далее проводят операцию быстрого дискретного преобразования Фурье с комплексными значениями 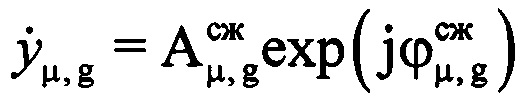 выборки, состоящей из 8-ми первых отсчетов массива Ни, в результате которого получают начальный низкоинформативный доплеровский спектр. Определяют в полученном начальном низкоинформативном доплеровском спектре частоту Доплера
выборки, состоящей из 8-ми первых отсчетов массива Ни, в результате которого получают начальный низкоинформативный доплеровский спектр. Определяют в полученном начальном низкоинформативном доплеровском спектре частоту Доплера 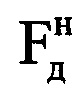 , которая соответствует максимальной по амплитуде составляющей спектра. Определяют радиальную скорость ВЦ в начале информативного интервала синтезирования
, которая соответствует максимальной по амплитуде составляющей спектра. Определяют радиальную скорость ВЦ в начале информативного интервала синтезирования  по формуле
по формуле 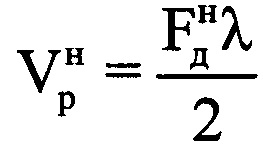 . Проводят операцию быстрого дискретного преобразования Фурье с комплексными значениями выборки, состоящей из 8-ми последних отсчетов массива Ни, в результате которого получают конечный низкоинформативный доплеровский спектр. Определяют в полученном конечном низкоинформативном доплеровском спектре частоту Доплера
. Проводят операцию быстрого дискретного преобразования Фурье с комплексными значениями выборки, состоящей из 8-ми последних отсчетов массива Ни, в результате которого получают конечный низкоинформативный доплеровский спектр. Определяют в полученном конечном низкоинформативном доплеровском спектре частоту Доплера 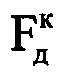 , которая соответствует максимальной по амплитуде составляющей спектра. Определяют радиальную скорость ВЦ в конце интервала синтезирования
, которая соответствует максимальной по амплитуде составляющей спектра. Определяют радиальную скорость ВЦ в конце интервала синтезирования 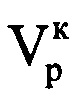 по формуле
по формуле 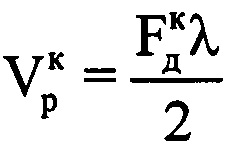 . Определяют среднюю радиальную скорость
. Определяют среднюю радиальную скорость 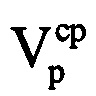 воздушной цели в пределах интервала синтезирования по формуле
воздушной цели в пределах интервала синтезирования по формуле 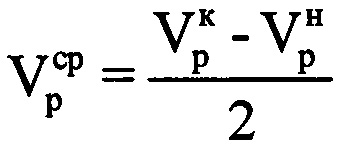 . Далее определяют радиальное ускорение ар ВЦ на выбранном информативном интервале синтезирования по формуле
. Далее определяют радиальное ускорение ар ВЦ на выбранном информативном интервале синтезирования по формуле 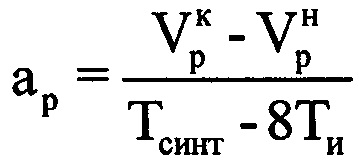 . Рассчитывают на основе полученных значений средней радиальной скорости
. Рассчитывают на основе полученных значений средней радиальной скорости 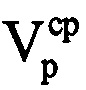 и ускорения ар величину компенсируемой фазы для каждого tμ-го момента времени, входящего в информативный интервал синтезирования по формуле
и ускорения ар величину компенсируемой фазы для каждого tμ-го момента времени, входящего в информативный интервал синтезирования по формуле 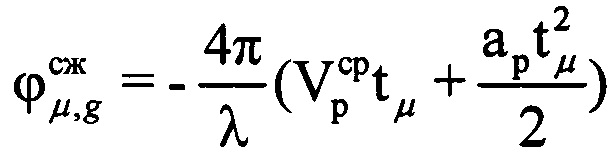 . Проводят компенсацию фазового влияния радиального движения ВЦ на информативном интервале синтезирования путем изменения фазы по формуле
. Проводят компенсацию фазового влияния радиального движения ВЦ на информативном интервале синтезирования путем изменения фазы по формуле 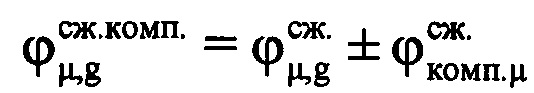 , где знак «-» соответствует движению ВЦ в направлении РЛС, т.е. приближению, а знак «+» соответствует удалению ВЦ. Создают в памяти ЭВМ РЛС четырехстрочный массив Нс (фиг. 12), в первую строку которого записывают номера μ-x периодов повторения с 1-го по М-й, во вторую - амплитуды
, где знак «-» соответствует движению ВЦ в направлении РЛС, т.е. приближению, а знак «+» соответствует удалению ВЦ. Создают в памяти ЭВМ РЛС четырехстрочный массив Нс (фиг. 12), в первую строку которого записывают номера μ-x периодов повторения с 1-го по М-й, во вторую - амплитуды 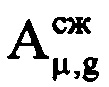 μ-х отсчетов ОХ, принадлежащих информативному интервалу синтезирования, в третью - скомпенсированные фазы
μ-х отсчетов ОХ, принадлежащих информативному интервалу синтезирования, в третью - скомпенсированные фазы 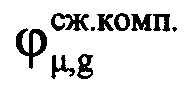 μ-х отсчетов ОХ, принадлежащих информативному интервалу синтезирования, в четвертую - моменты времени tμ, соответствующие амплитудам и фазам отраженных сигналов в μ-x периодах повторения. Для осуществления быстрого дискретного преобразования Фурье полученный массив дискретных отсчетов расширяют путем ввода новых элементов с нулевыми значениями амплитуд и фаз, добиваясь числа элементов массива Нс, равного Е=2m, где Е - ближайшее целое число, удовлетворяющее условию Е=2m и Е>М, m - целое число. Проводят операцию быстрого дискретного преобразования Фурье с вектором комплексных величин
μ-х отсчетов ОХ, принадлежащих информативному интервалу синтезирования, в четвертую - моменты времени tμ, соответствующие амплитудам и фазам отраженных сигналов в μ-x периодах повторения. Для осуществления быстрого дискретного преобразования Фурье полученный массив дискретных отсчетов расширяют путем ввода новых элементов с нулевыми значениями амплитуд и фаз, добиваясь числа элементов массива Нс, равного Е=2m, где Е - ближайшее целое число, удовлетворяющее условию Е=2m и Е>М, m - целое число. Проводят операцию быстрого дискретного преобразования Фурье с вектором комплексных величин 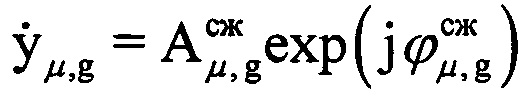 из массива Нс. Получают массив Ндоп, содержащий Е комплексных значений спектра отраженного сигнала, который представляет собой доплеровский портрет ВЦ, полученный на информативном интервале синтезирования Тс [5]. В полученном массиве Ндоп, характеризующем доплеровский портрет, определяют крайний левый и крайний правый максимумы путем перебора и анализа амплитудных значений элементов массива Ндоп. Далее записывают в память ЭВМ РЛС номера отсчетов iнmax и iкmax в массиве Ндоп, соответствующих начальному и конечному максимумам. Вычисляют частотную протяженность доплеровского портрета по формуле ΔF=(iкmax-iнmax)/Tc. С помощью цифровой вычислительной системы по известным формулам сферические координаты ВЦ 1-го и I-го периода повторения пересчитывают в прямоугольные координаты х, у, z соответствующих периодов повторения х1, y1, z1 и xI, yI, zI. Далее рассчитывают расстояние r, которое преодолела ВЦ за время регистрации отраженных сигналов по формуле
из массива Нс. Получают массив Ндоп, содержащий Е комплексных значений спектра отраженного сигнала, который представляет собой доплеровский портрет ВЦ, полученный на информативном интервале синтезирования Тс [5]. В полученном массиве Ндоп, характеризующем доплеровский портрет, определяют крайний левый и крайний правый максимумы путем перебора и анализа амплитудных значений элементов массива Ндоп. Далее записывают в память ЭВМ РЛС номера отсчетов iнmax и iкmax в массиве Ндоп, соответствующих начальному и конечному максимумам. Вычисляют частотную протяженность доплеровского портрета по формуле ΔF=(iкmax-iнmax)/Tc. С помощью цифровой вычислительной системы по известным формулам сферические координаты ВЦ 1-го и I-го периода повторения пересчитывают в прямоугольные координаты х, у, z соответствующих периодов повторения х1, y1, z1 и xI, yI, zI. Далее рассчитывают расстояние r, которое преодолела ВЦ за время регистрации отраженных сигналов по формуле 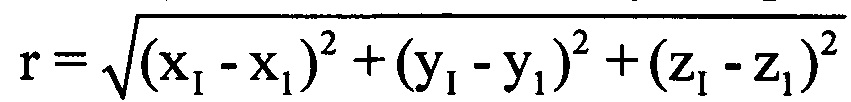 . С помощью цифровой вычислительной системы рассчитывают путевую скорость ВЦ V по формуле
. С помощью цифровой вычислительной системы рассчитывают путевую скорость ВЦ V по формуле 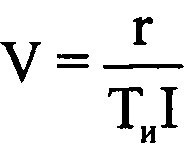 . Рассчитывают курсовой угол ВЦ γ по формуле
. Рассчитывают курсовой угол ВЦ γ по формуле 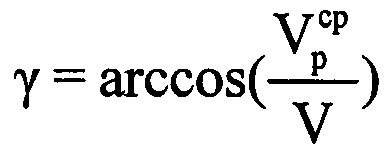 (фиг. 13). Выбирают значение дальности, соответствующее серединному отсчету в интервале регистрации данных, равное RI/2, на основе чего рассчитывают уточненное значение угловой скорости
(фиг. 13). Выбирают значение дальности, соответствующее серединному отсчету в интервале регистрации данных, равное RI/2, на основе чего рассчитывают уточненное значение угловой скорости 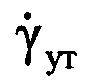 поворота ВЦ относительно РЛС по формуле
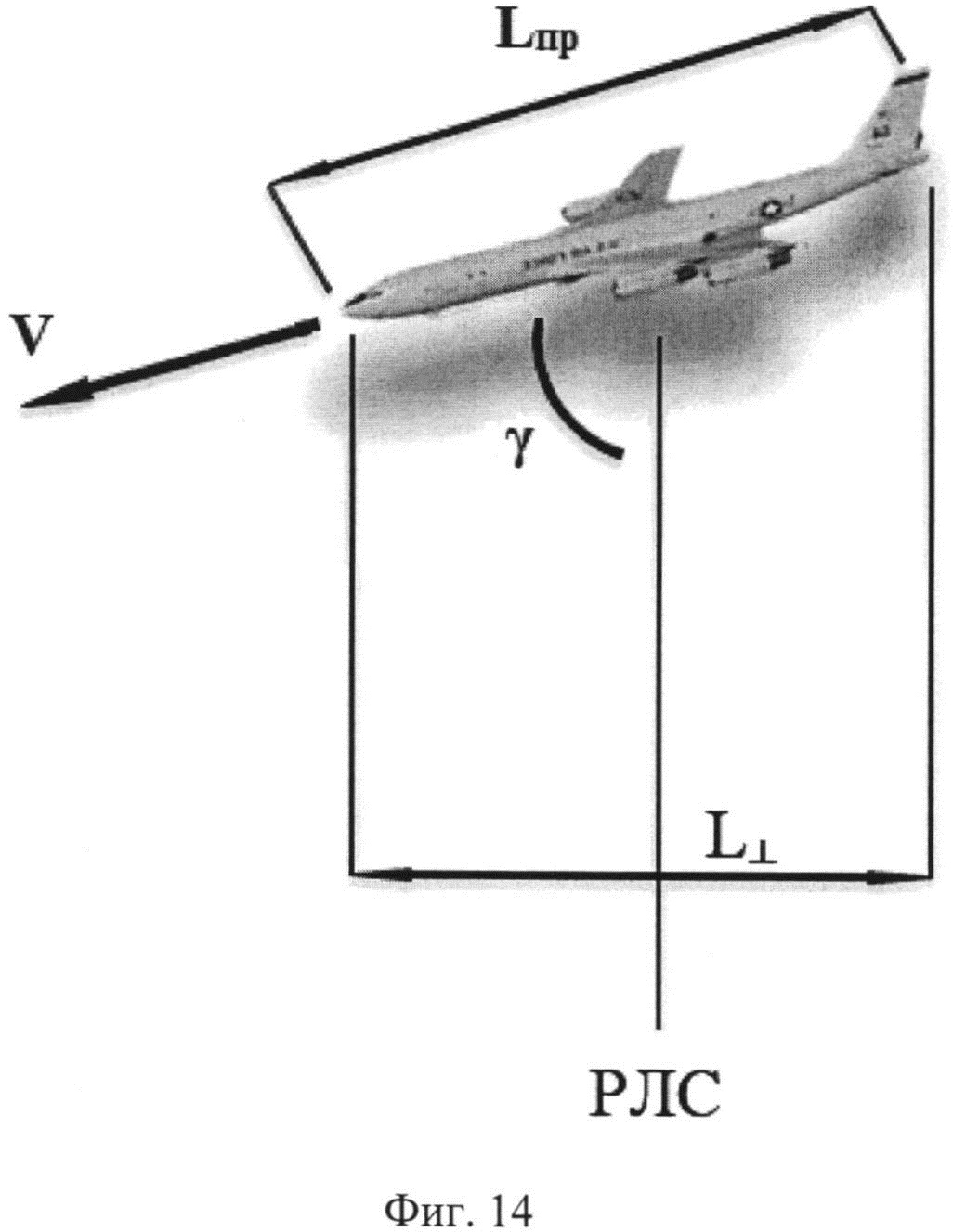
поворота ВЦ относительно РЛС по формуле 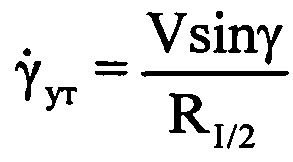 . На основе рассчитанных данных определяют пространственный размер Lпр ВЦ по формуле
. На основе рассчитанных данных определяют пространственный размер Lпр ВЦ по формуле 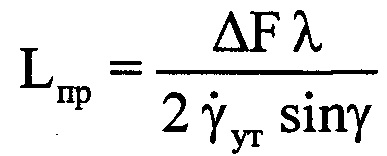 (фиг. 14).
(фиг. 14).
Сущность изобретения заключается в следующем. Современные РЛС имеют возможность измерять большое число параметров ВЦ, а для оценки размера ВЦ ранее использовалось ограниченное число параметров. К параметрам, учет которых может обеспечить уточнение размера ВЦ, относятся координаты ВЦ, ее путевая скорость, угловая скорость поворота относительно РЛС, текущая (изменяемая во времени) дальность и др. Способ предполагает учет этих дополнительных параметров при расчете пространственного размера ВЦ по протяженности ее ДпП.
Процесс уточнения величины пространственного размера Lпр можно пояснить следующими расчетными выражениями. Для расчета Lпр, как показано выше, может быть использована формула 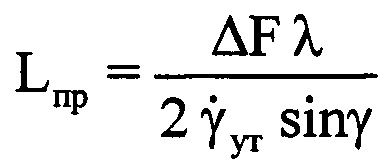 . В нее входит уточненное значение угловой скорости поворота ВЦ
. В нее входит уточненное значение угловой скорости поворота ВЦ 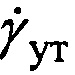 . Для получения величины уточненной угловой скорости поворота
. Для получения величины уточненной угловой скорости поворота 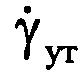 ВЦ относительно РЛС может быть использована формула
ВЦ относительно РЛС может быть использована формула 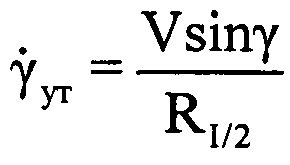 . В ней используется величина дальности до ВЦ. Поскольку дальность на интервале регистрации данных меняется, для расчета
. В ней используется величина дальности до ВЦ. Поскольку дальность на интервале регистрации данных меняется, для расчета 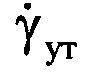 целесообразно использовать дальность, соответствующую середине интервала регистрации. А для этого необходимо из сигналов системы измерения дальности, пропорциональных дальности до ВЦ, с помощью АЦП получать для каждого i-го периода повторения цифровое значение дальности Ri, что и предполагает новый способ. Далее выбирают среднее за интервал регистрации значение дальности Rcp, соответствующее серединному отсчету в интервале регистрации данных Rcp=RI/2.
целесообразно использовать дальность, соответствующую середине интервала регистрации. А для этого необходимо из сигналов системы измерения дальности, пропорциональных дальности до ВЦ, с помощью АЦП получать для каждого i-го периода повторения цифровое значение дальности Ri, что и предполагает новый способ. Далее выбирают среднее за интервал регистрации значение дальности Rcp, соответствующее серединному отсчету в интервале регистрации данных Rcp=RI/2.
В интересах более корректного формирования ОХ ВЦ величины амплитуд и фаз целесообразно извлекать из точек, соответствующих пикам откликов отраженного сигнала. А пик отклика от периода к периоду перемещается в соответствии с изменением дальности. Поэтому для каждого периода повторения рассчитывают время прохождения излученного сигнала до ВЦ и обратно по формуле 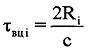 . На основании этого для каждого i-го периода повторения определяют номер отсчета gi оцифрованного отраженного сигнала, на который при дальности до воздушной цели Ri будет приходиться пик отклика отраженного сигнала после согласованной фильтрации. Для расчета номера отсчета gi отраженного сигнала i-го периода повторения, из которой следует извлекать значение амплитуды и фазы отражений в i-м периоде, предложено использовать формулу
. На основании этого для каждого i-го периода повторения определяют номер отсчета gi оцифрованного отраженного сигнала, на который при дальности до воздушной цели Ri будет приходиться пик отклика отраженного сигнала после согласованной фильтрации. Для расчета номера отсчета gi отраженного сигнала i-го периода повторения, из которой следует извлекать значение амплитуды и фазы отражений в i-м периоде, предложено использовать формулу  .
.
Для расчета (получения) путевой скорости V ВЦ из сигналов канала угловой автоматики РЛС, пропорциональных углу места ε и азимуту β ВЦ, с помощью соответствующих АЦП в каждом i-м периоде повторения получают цифровые отсчеты угла места εi и азимута βi. По известным формулам сферические координаты первого и I-го периодов повторения пересчитывают в прямоугольные координаты х, y, z соответствующих периодов повторения x1, y1, z1 и xI, yI, zI, на основе чего рассчитывают расстояние r, которое преодолела ВЦ за время регистрации отраженных сигналов по формуле 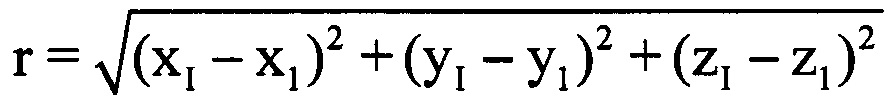 . Расчет путевой скорости V ВЦ предложено проводить по формуле
. Расчет путевой скорости V ВЦ предложено проводить по формуле 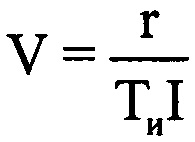 , для чего имеются все необходимые величины. Для получения величины курсового угла γ предложено использовать формулу
, для чего имеются все необходимые величины. Для получения величины курсового угла γ предложено использовать формулу 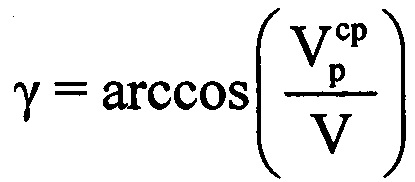 , внутренние переменные которой известны.
, внутренние переменные которой известны.
Значение ракурса ВЦ γ необходимо для пересчета поперечного размера ВЦ L⊥ в ее пространственный размер Lпр по формуле Lпр=L⊥/sinγ, что в общем виде эквивалентно расчету по формуле
Способ легко реализуем за счет обработки отраженных сигналов в цифровом виде. Способ не требует введения в структуру радиолокационной станции новых элементов, вследствие чего является осуществимым на современном уровне развития техники. Извлекаемый из ДпП признак идентификации ВЦ в виде ее пространственного размера может быть использован в существующих радиолокационных станциях сопровождения для классификации и идентификации воздушных целей как автономно, так и в качестве дополнительного признака в совокупности с другими. Это, в свою очередь, может привести к улучшению информационных возможностей радиолокационной системы, используемой, к примеру, на аэродромах при контроле воздушного движения по трассовым коридорам пролета.
Источники информации
1. Патент РФ №2562060 от 7.08.2015 г. Способ извлечения из доплеровских портретов воздушных объектов признаков идентификации с использованием метода сверхразрешения. Романенко А.В., Митрофанов Д.Г. и др. Заявка №2014125641 от 24.06.2014 г. МПК G01S 13/90.
2. Митрофанов Д.Г., Прохоркин А.Г., Нефедов С.И. Измерение поперечных размеров летательных аппаратов по частотной протяженности доплеровского портрета // Радиотехника, 2008. №1. С. 84-90 (прототип).
3. Кирьянов Д.В., Mathcad 13, СПб., БХВ-Петербург, 2006. 608 с.
4. Селекция и распознавание на основе локационной информации / Под ред. А.Л. Горелика. М., Радио и связь, 1990. 240 с.
5. Комплексный адаптивный метод построения радиолокационных изображений в системах управления двойного назначения // Теория и системы управления. Известия РАН, 2006. №1. С. 101-118.
6. Митрофанов Д.Г. Метод построения радиолокационных изображений аэродинамических летательных аппаратов // Полет, 2006. №11. С. 52-60.
7. Радиолокационные характеристики летательных аппаратов / Под ред. Л.Т. Тучкова. М., Радио и связь, 1985. 236 с.
8. Митрофанов Д.Г. Влияние амплитудного и фазового шума на качество формирования радиолокационного изображения // Радиотехника и электроника, 1995. Т. 40. №4. С. 586-590.
9. Патент РФ №2066059. МПК G01S 13/89. Способ построения двумерного радиолокационного изображения в РЛС сопровождения прямолинейно движущейся цели / Митрофанов Д.Г. БИ №24, 1996.
10. Патент РФ №2099742. МПК G01S 13/89. Триангуляционный способ построения двумерного радиолокационного изображения цели в РЛС сопровождения с инверсным синтезированием апертуры / Митрофанов Д.Г. БИ №35, 1997.
11. Митрофанов Д.Г. Развитие методов формирования доплеровских портретов и двумерных радиолокационных изображений воздушных целей // Оборонная техника, 1998. №10-11. С. 75-81.
12. Митрофанов Д.Г. Синтез радиолокационного изображения цели методом математического моделирования ее доплеровских портретов. Киев, Радиоэлектроника. Известия вузов, 1994. Т. 37. №3. С. 72-76.
13. Митрофанов Д.Г. Формирование двумерного радиолокационного изображения цели с траекторными нестабильностями полета // Радиотехника и электроника. РАН, 2002. Т. 47. №7. С. 852-859.
14. Митрофанов Д.Г. Построение двумерного изображения объекта с использованием многочастотного зондирующего сигнала // Измерительная техника. 2001. №2. С. 57-62.
15. Митрофанов Д.Г. Развитие способа выбора интервала инверсного синтезирования при наличии траекторных нестабильностей полета воздушного объекта. Сборник докладов XVII международной НТК «RLNC-2011». 2011. Воронеж: НПФ «САКВОЕЕ» ООО. С. 2251-2258.
16. Радиолокационные системы. Справочник. Основы построения и теория / Под ред. Я.Д. Ширмана. М., Радиотехника, 2007. 510 с.
17. Небабин В.Г., Сергеев В.В. Методы и техника радиолокационного распознавания. - М.: Радио и связь, 1984.
18. Финкельштейн М.И. Основы радиолокации. М., Сов. радио, 1973. 496 с.