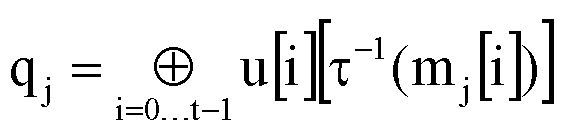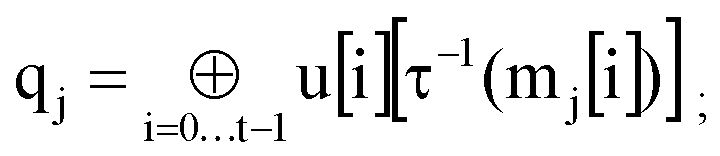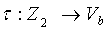Результат интеллектуальной деятельности: СПОСОБ КРИПТОГРАФИЧЕСКОГО ПРЕОБРАЗОВАНИЯ
Вид РИД
Изобретение
Область техники, к которой относится изобретение
Предлагаемое изобретение относится к криптографии и средствам защиты информации и может быть использовано для реализации блочного шифрования, хэш-функций, генераторов псевдослучайных последовательностей и т.д.
Уровень техники
Известны способы итерационного криптографического преобразования сообщений фиксированной длины, представленных в цифровом виде, а именно в виде двоичных данных, выполняемые с использованием секретного ключа, например способ, реализованный в виде алгоритма блочного шифрования AES (Advanced Encryption Standard) [1].
Алгоритм блочного шифрования AES включает два этапа использования: зашифрование и расшифрование. На обоих этапах формируются раундовые ключи шифрования, вычисляемые при помощи секретного ключа. Сообщения фиксированной длины преобразуются путем последовательного выполнения над ними обратимых линейных и нелинейных операций и побитового суммирования сообщения с раундовыми ключами. В качестве линейных операций используются перестановка байтов сообщения и умножение сообщения на фиксированную матрицу. В качестве нелинейных операций используются операции побайтовой подстановки. На этапе зашифрования после каждого нелинейного преобразования применяется линейное преобразование. На этапе расшифрования используются обратные преобразования, и они применяются в обратном порядке: после каждого линейного преобразования следует нелинейное преобразование.
Введем обозначения:
- Vh - множество всех двоичных векторов длины h;
- m - сообщение (двоичный вектор) длины w;
- n - количество итерационных ключей, причем n>2;
- w - размер сообщения в битах, причем w=b·t,
где t, b∈N (множество натуральных чисел);
- с - сообщение (двоичный вектор) длины w;
-  - взаимно-однозначное преобразование, которое ставит в соответствие целому числу из промежутка 0, …, 2b-1 вектор его двоичного представления, младшие биты числа находятся справа.
- взаимно-однозначное преобразование, которое ставит в соответствие целому числу из промежутка 0, …, 2b-1 вектор его двоичного представления, младшие биты числа находятся справа.
- А||В - операции конкатенации двух векторов А и В, результатом является вектор, в котором левая часть совпадает с вектором А, а правая часть совпадает с вектором В;
- X[K] - линейное преобразование, зависящее от итерационного ключа K, причем
X[K]:Vw→Vw,
X[K](a)=K⊕a,
где а - это сообщение (двоичный вектор) длины w,
K∈Vw;
- S - нелинейное взаимно-однозначное преобразование, причем
S:Vw→Vw,
S(a)=S(a t-1||…||a 0)=π(a t-1)||…||π(a 0),
где а∈Vw,
a=a t-1||…||a 0,
ai∈Vb,
π - любое взаимно-однозначное преобразование, причем
π:Vb→Vb
- L1 - линейное взаимно-однозначное преобразование, причем
L1:Vw→Vw;
- L2 - линейное взаимно-однозначное преобразование, причем
L2:Vw→Vw;
- L - линейное взаимно-однозначное преобразование, причем
L:Vw→Vw;
L(a)=a·D,
где D - невырожденная матрица размером w×w;
G=D-1 - обратная матрица по отношению к D;
Gi - матрица размера b×w, состоящая из подряд расположенных строк матрицы G с номерами
(t-1-i)·b+1, (t-1-i)·b+2, …, (t-i)·b,
где i=0, …, t-1, a∈Vw;
L является композицией линейных преобразований L1 и L2:
L(a)=L1(L2(a)).
В указанных обозначениях алгоритм зашифрования AES запишется в виде
c=X[Kn]L2S…X[K1]LSX[K0](m),
а алгоритм расшифрования:
m=X[K0]S-1L-1…S-1L-1X[Kn-1]S-1L2 -1X[Kn](c),
где Ki - раундовые ключи Ki∈Vw, i=0, …, n.
Известен способ реализации алгоритма зашифрования, использующего композицию преобразований LS (сначала выполняется S, потом - L), на универсальных вычислительных платформах с достаточным количеством памяти. Основная идея способа заключается в объединении данных преобразований в одно и его табличная реализация. Этот способ описан, например, в работах [2, 3].
Алгоритм расшифрования требует выполнения композиции преобразований S-1L-1 (сначала L-1, потом - S-1). Такой способ объединения этих преобразований и его табличная реализация в общем случае практически неприменимы из-за чрезвычайного большого объема таблиц, что является его недостатком.
Раскрытие изобретения
Техническим результатом является увеличение скорости обработки информации и снижение количества операций при реализации итерационного криптографического преобразования.
Заявленный результат достигается за счет замены исходной композиции преобразований эквивалентными преобразованиями с последующей их эффективной реализацией.
Отметим, что для одной итерации в силу линейности преобразования L-1 для любого сообщения а, справедливо соотношение
L-1X[Ki]S-1(a)=L-1X[Ki](S-1(a))=L-1(S-1(a)⊕Ki)=L-1(S-1(a))⊕L-1(Ki)=L-1S-1(a)⊕L-1(Ki)=X[L-1(Ki)]L-1S-1(a)
Тогда исходное итерационное криптографическое преобразование
m=X[K0]S-1L-1…S-1L-1X[Kn-1]S-1L-1X[Kn](c)
заменяется эквивалентным, в котором S-1 предшествует L-1:
m=X[KZ0]S-1X[KZ1]L-1S-1…X[KZn-1]L-1S-1X[KZn]L-1S-1S(c),
где KZ0=K0,
а остальные вычисляются по формуле
KZj=L-1(Kj),
где j=1, …, n
Такое представление потребует вычислить новые итерационные ключи, как показано выше.
Таким образом, применение композиции S-1L-1 сводится к применению композиции L-1S-1, реализация которой требует такого же количества вычислительных ресурсов, что и реализация LS, а значит, эффективно реализуется указанным в работах [2, 3] способом и по сложности эквивалентна преобразованию L.
Рассмотрим композицию Y преобразований L-1 и S-1
Y(a)=L-1(S-1(a))
Сначала к сообщению а применяется преобразование
S-1(a)=S-1(a t-1||…||a 0)=π-1(a t-1)||…||π-1(a 0),
в результате получается новое сообщение (двоичный вектор)
d=S-1(a)
Затем над вектором d выполняется линейное преобразование, которое эквивалентно умножению вектора d на заданную матрицу G, которая соответствует линейному преобразованию L-1
L-1S-1(a)=d·G
Вектор d разбивается на части
d=dt-1||…||d0
и для каждого значения части вычисляется промежуточный вектор

где i=0, …, t-1;
j=0, …, 2b-1
Для вычисления результата умножения вектора d на матрицу G необходимо сложить соответствующие промежуточные векторы


Учитывая, что
d=(dt-1||…||d0)=(π-1(a t-1)||…||π-1(a0)),
из (1) получаем

Для того чтобы исключить преобразования π-1, нужно вычислить соответствующие промежуточные значения

Отметим связь значений

Тогда из (2) получаем

Описанный способ позволяет объединить два преобразования L-1 и S-1 в одно, по сложности равное одному преобразованию L.
Проведем сравнительную оценку известного и предложенного способов.
Способ непосредственной реализации криптографического преобразования, согласно известному выражению
m=X[K0]S-1L-1…X[Kn-1]S-1L-1X[Kn](c)
требует выполнения n раз преобразований, по сложности равных преобразованиям L, выполнения n раз преобразований типа S и выполнения n+1 раз преобразований типа X[Ki].
Реализация криптографического преобразования предложенным способом, согласно выражению
m=X[KZ0]S-1X[KZ1]L-1S-1…X[KZn-1]L-1S-1X[KZn]L-1S-1S(c),
требует выполнения n раз преобразований, по сложности равных преобразованиям L, двух преобразований типа S и выполнения n+1 раз преобразований типа X[KZi], также необходимо однократно вычислить новые итерационные ключи
KZ0=K0,
KZi=L-1(Ki),
где i=1, …, n,
что потребует выполнения n раз преобразований типа L.
Если для выполнения операции типа L требуется l тактов процессора, а для выполнения операции чипа S необходимо s тактов процессора, то получаем, что предложенный способ становится быстрее известного исходного преобразования, если происходит обработка количества сообщений длины w большего, чем целая часть от величины

при условии, что итерационные ключи при этом остаются неизменными и вычисляются только один раз для всех сообщений длины w.
Отметим также, что в предлагаемом способе можно выполнить на одно преобразование типа S меньше, но это приведет к тому, что при вычислении будут использоваться два разных преобразования, по сложности равных преобразованиям L: первое преобразование L-1S-1, второе L-1. Тогда преобразование примет вид
m=X[KZ0]S-1X[KZ1]L-1S-1…X[KZn-1]L-1S-1X[KZn]L-1(c),
и оно потребует выполнения n раз преобразований по сложности равных преобразованиям L, одного преобразования типа S и n+1 раз преобразований типа X[Ki].
Рассматриваемый класс итерационных криптографических преобразований реализует так называемую подстановочно-перестановочную сеть, широко используемую при создании криптографических алгоритмов. В частности, на основе таких преобразований могут быть построены блочные шифры, криптографические хэш-функции, генераторы псевдослучайных последовательностей и другие криптографические примитивы.
Осуществление изобретения
Рассмотрим осуществление предложенного способа на примере блочного шифра, по своей структуре совпадающего с AES. Отличие заключается в том, что при шифровании последнее линейное преобразование L2 заменяется преобразованием L, то есть дополнительно добавляется преобразование L1 для сохранения единообразия линейного преобразования.
Тогда алгоритм зашифрования сообщения (двоичного вектора) m длины 128 бит в двоичный вектор c также длины 128 бит будет иметь вид (известно, что при зашифровании по стандарту AES используется в совокупности 15 итерационных ключей при длине исходного секретного ключа 256 бит):
c=X[K14]LS…X[K1]LSX[K0](m),
а алгоритм расшифрования:
m=[K0]S-1L-1…X[K13]S-1L-1X[K14](c)
Покажем, как осуществить алгоритм расшифрования предложенным способом. Считаем, что итерационные ключи заданы.
Сначала выбирают преобразования из допустимых множеств:
Vh - множество всех двоичных строк длины h,
X[Ki]:V128→V128 задается следующим образом:
X[Ki](a)=Ki⊕a,
где Ki - итерационный ключ исходного криптографического преобразования, причем Ki, a∈V128, i=0, …, 14;
L:V128→V128 - линейное взаимно-однозначное преобразование однозначно определяется заданием невырожденной двоичной матрицы D размера 128×128.
L(a)=a·D,
обратная матрица
G=D-1;
S:V128→V128 - нелинейное взаимно-однозначное преобразование, причем
a=a 15||…||a 0,
где a i∈V8;
S(a)=S(a 15||…||a 0)=π(a 15)||…||π(a 0),
где π:V8→V8 - любое взаимно-однозначное преобразование, оно однозначно определяет преобразование S(а),
τ:Z256→V8 - взаимно-однозначное преобразование, которое ставит в соответствие целому числу из промежутка 0…255 вектор его двоичного представления, младшие биты числа находятся справа.
Затем вычисляют новые итерационные ключи KZ0, …, KZ14 на основе имеющегося набора итерационных ключей K0, …, K14, причем нулевой ключ в новом наборе определяют по формуле
KZ0=K0,
а остальные по формуле
KZj=L-1(Kj),
где j=1, …, 14.
После этого вычисляют двоичные векторы u[i][j] длины 128 бит, по формуле
u[i][j]=π-1(τ(j))·Gi,
где Gi - матрица, состоящая из подряд расположенных строк матрицы G, которая соответствует линейному преобразованию L-1, с номерами (15-i)·8+1, (15-i)·8+2, …, (16-i)·8, где i=0, …, 15; j=0, …, 255.
В завершении вычисляют m:
m14=S(c);
 ,
,
mj-1=X[KZj](qj),
где
mj=mj[15]||mj[14]||…||mj[0];
j=14, …, 1,
m=X[KZ0](S-1(m0)).
Для реализации всех вычислений и операций вполне может быть сформирована программа (комплекс программ) специалистом по программированию (программистом) на любом известном универсальном языке программирования (например, языке С) на основе приведенных выше соотношений. Затем эта программа может быть выполнена на компьютере.
В приводимом примере n=14. Подставив это значение в формулу (3), получаем, что предложенный способ становится быстрее исходного преобразования, если происходит обработка количества сообщений длины 128 бит большего, чем целая часть

при условии, что итерационные ключи при этом остаются неизменными и вычисляются только один раз для всех сообщений длины 128 бит.
Необходимо отметить, что возможны и другие варианты реализации предложенного способа, отличающиеся от описанного выше и зависящие от личных предпочтений при программировании отдельных действий и функций.
Источники информации
1. National Institute of Standards and Technology, U.S. Department of Commerce. "Advanced Encryption Standard", Federal Information Processing Standards Publication 197, Washington, DC, November 2001.
2. П.А. Лебедев. Сравнение старого и нового стандартов РФ на криптографическую хэш-функцию на ЦП и графических процессорах NVIDIA. Математические вопросы криптографии, том 4, вып. 2, 2013, с. 73-80.
3. О. Kazymyrov, V. Kazymyrova, Algebraic Aspects of the Russian Hash Standard COST R 34.11-2012, 2nd Workshop on Current Trends in Cryptology (CTCrypt 2013) June 23-25. 2013. pp. 160-176.
Способ криптографического преобразования сообщения с, представленного в двоичном виде, заключающийся в том, что вычисляют на основе имеющегося набора итерационных ключей K, …, K новый набор итерационных ключей KZ, …, KZ, причем нулевой ключ в новом наборе определяют по формуле KZ=K, а остальные по формуле KZ=L(K), где j=1, …, n; L - линейное взаимно-однозначное преобразование, причем L:V→V; L()=·D, где V - множество всех двоичных строк длины n,w - размер сообщения в битах, причем w=b·t,где t, b∈N (множество натуральных чисел);D - невырожденная матрица размером w×w; - сообщение (двоичный вектор) длины w;KZ, K∈V,где i=0, …, n;вычисляют двоичные векторы u[i][j] длины w по формулеu[i][j]=π(τ(j))·G,где j=0, …, 2-1;G - матрица размером b×w, состоящая из подряд расположенных строк матрицы G с номерами (t-1-i)·b+1, (t-1-i)·b+2, …, (t-i)·b;i=0, …, t-1;G=D - обратная матрица по отношению к D: - взаимно-однозначное преобразование, которое ставит в соответствие целому числу из промежутка 0, …, 2-1 вектор его двоичного представления, младшие биты числа находятся справа;π - любое взаимно-однозначное преобразование, причемπ:V→V;вычисляют двоичный вектор m длины w, используя новые итерационные ключи KZ, …, KZ, выполняя следующие действия:вычисляютm=S(),где S - нелинейное взаимно-однозначное преобразование, причемS:V→V, = ||…|| ,где ∈V;S()=S( ||…|| )=π( )||…||π( );вычисляют m=X[KZ](q),где m=m[t-1]||m[t-2]||…||m[0];j=n, …, 1;X[KZ] - линейное преобразование, зависящее от итерационного ключа KZ, причемX[KZ]:V→V,X[KZ]()=KZ⊕,где KZ, ∈V;вычисляютm=X[KZ](S(m)).