Результат интеллектуальной деятельности: СИСТЕМА И СПОСОБ ОПРЕДЕЛЕНИЯ АМПЛИТУДЫ И ФАЗОВОЙ ЗАДЕРЖКИ СИНУСОИДАЛЬНОГО СИГНАЛА
Вид РИД
Изобретение
Настоящее изобретение относится к системе и способу определения амплитуды и фазовой задержки синусоидального сигнала.
В настоящем описании фазовой задержкой синусоидального сигнала называют значение, противоположное значению фазы этого сигнала, для исходного момента, называемого также первоначальным моментом и соответствующего t=0, где t обозначает переменную времени.
Многие приложения требуют характеризовать сигнал по его амплитуде и по его фазовой задержке. В частности, это относится к случаю, когда необходимо характеризовать реакцию резонатора на сигнал возбуждения, при этом резонатор может входить в состав виброакселерометра или виброгироскопа.
Для этого чаще всего синусоидальный сигнал оцифровывают, затем анализируют, например, при помощи преобразования Фурье. Однако оцифровку сигнала, включая его дискретизацию в определенные моменты и квантование значений сигнала, которые являются действительными в эти моменты, производят, используя аналого-цифровые преобразователи, которые являются комбинированными электронными компонентами, выполненными по специфической полупроводниковой технологии. Следовательно, аналого-цифровые преобразователи следует подвергнуть серьезной доработке, чтобы их можно было применять в космической отрасли, что повышает их себестоимость.
Кроме того, чтобы избежать этих недостатков аналого-цифровых преобразователей, в документе US 5,166,959 было предложено характеризовать синусоидальный сигнал, фиксируя моменты приведения к нулю этого сигнала. Но такой метод не позволяет определить амплитуду синусоидального сигнала, а только его фазовую задержку, и он не является точным, когда амплитуда сигнала является слабой и/или когда отношение сигнала к шуму является незначительным.
В документе WO 2008/022653 раскрыта система измерения синусоиды, которая основана на датах сравнения идентифицируемого сигнала с контрольным сигналом.
С другой стороны в статье R. Micheletti, озаглавленной "Phase Angle Measurements Between Two Sinusoidal Signals" (Измерения фазового угла между двумя синусоидальными сигналами), IEEE Trans. Instr. Meas. Vol. 40, No. 1, 1st February 1991, pp. 40–42, XP055353815, предлагается алгоритм измерения фазового угла между двумя сигналами. Алгоритм основан на методе наименьших квардаров и реализуется на цифровых сигналах.
Наконец, в статье B. Maréchal et al., озаглавленной "Direct Digital Synthetizer (DDS) design parameters optimization for vibrating MEMS sensors" (Оптимизация параметров конструкции прямого цифрового синтезатора (DDS) для вибрирующих датчиков MEMS), 2014 SYPMOSIUM ON DESIGN, TEST. INTEGRATION AND PACKAGING OF MEMS/MOEMS (DTIP), CIRCUITS MULTI PROJETS – CMP 1st April 2014, pp. 1–5, XP032746454, предлагается оптимизированная конструкция блоков синтеза цифрового сигнала.
С учетом этой ситуации изобретение призвано предложить новый способ определения амплитуды и фазовой задержки синусоидального сигнала, не требующий применения аналого-цифрового преобразователя.
Дополнительной задачей изобретения является создание системы, которая выполнена с возможностью определять амплитуду и фазовую задержку синусоидального сигнала, которая является недорогой и которую можно применять для космических приложений с небольшими затратами.
Еще одной задачей изобретения является создание системы, большую часть которой можно распределить между несколькими каналами, каждый из которых предназначен для определения амплитуды и фазовой задержки синусоидального сигнала, отличного от синусоидального сигнала других каналов, при этом все каналы работают постоянно и одновременно.
Наконец, изобретение призвано также предложить такую систему, которая является точной даже для синусоидального сигнала слабой амплитуды, возможно наложенного на шум.
Для достижения по меньшей мере одной из этих целей первым объектом изобретения является система для определения значения амплитуды и значения фазовой задержки, относящихся к измеряемому сигналу, который имеет синусоидальные изменения в зависимости от времени с частотой F, причем эта система содержит:
- блок синтеза, выполненный с возможностью генерировать контрольный сигнал, который имеет синусоидальную форму временных изменений, находящуюся в постоянной фазовой взаимосвязи с измеряемым сигналом, причем этот контрольный сигнал имеет амплитуду, большую, чем амплитуда измеряемого сигнала, и имеет частоту, равную Fref = F x P/Q, где P и Q являются двумя фиксированными не равными нулю положительными целыми числами, при этом Р больше, чем Q,
- компаратор, который подсоединен, чтобы принимать на одном из своих входов измеряемый сигнал и контрольный сигнал, и который выполнен с возможностью выдавать на выходе переходный сигнал в каждый момент, когда измеряемый сигнал становится меньше, чем контрольный сигнал, или в каждый момент, когда измеряемый сигнал становится больше, чем контрольный сигнал;
- сдвиговый регистр, который подсоединен, чтобы принимать моментальные значения фазы контрольного сигнала на своем входе данных и чтобы принимать сигнал, выдаваемый на выходе компаратором, на своем входе валидации, и который выполнен с возможностью выбирать те значения фазы контрольного сигнала, которые принимаются регистром одновременно с переходным сигналом, выдаваемым компаратором, при этом компаратор и регистр образуют канал считывания для измеряемого сигнала; и
- вычислительный блок, который подсоединен, чтобы принимать выбранные значения фазы контрольного сигнала, и выполнен с возможностью вычислить значения амплитуды и фазовой задержки измеряемого сигнала на основании этих выбранных значений фазы контрольного сигнала.
Таким образом, заявленная система работает посредством идентификации значений фазы контрольного сигнала, при которых измеряемый сигнал становится меньше, чем контрольный сигнал, или больше, чем этот контрольный сигнал. На основании этих значений фазы вычислительный блок определяет амплитуду и фазовую задержку измеряемого сигнала.
Таким образом, заявленная система не использует никакого аналого-цифрового преобразователя, чтобы определять амплитуду и фазовую задержку измеряемого синусоидального сигнала.
Блок синтеза контрольного сигнала и сдвиговый регистр являются простыми и недорогими цифровыми компонентами, которые можно применять без существенных доработок для космических приложений, поскольку базовые цифровые функции уже применяются в данной технологии. Что касается компаратора, то хотя здесь речь идет о смешанной функции, но она не создает трудности и может сводиться к простой дифференциальной паре транзисторов.
Это же относится и к вычислительному блоку, который может содержать или может быть выполнен в виде специальной схемы или в виде интегральной схемы специального назначения, обозначаемой аббревиатурой ASIC, или в виде программируемой схемы, обозначаемой аббревиатурой FPGA, для которых реализуемые уровни интеграции существенно повысились в эти последние годы, в то время как их стоимость значительно снизилась. Действительно, амплитуду и фазовую задержку измеряемого сигнала можно вычислить, в основном выполняя операции сложения, умножения и вычитания чисел, в том числе со значениями чисел, которые являются фиксированными и которые, следовательно, можно предварительно записать в памяти. Как известно, разработку и описание вычислительного блока в виде ASIC или FPGA можно осуществлять очень гибко и экономично на таких языках как VHDL или Verilog. В целом, в рамках изобретения по меньшей мере один среди блока синтеза, сдвигового регистра и вычислительного блока предпочтительно можно выполнить в виде такой специальной схемы (ASIC) или в виде такой программируемой логической схемы (FPGA).
Наконец, учитывая, что отмечаемые моменты относятся к сравнению измеряемого сигнала с переменным контрольным сигналом, точность, с которой можно определять эти моменты, может быть достаточной, даже если измеряемый сигнал имеет амплитуду, которая является небольшой и которую искажает шум.
В предпочтительных вариантах выполнения изобретения число Р может быть равно числу Q, увеличенному на единицу : P = Q + 1.
В целом, в рамках изобретения вычислительный блок может быть выполнен с возможностью вычислять значение синфазной амплитуды измеряемого сигнала, равное а⋅cosФ, где Ф является значением фазовой задержки измеряемого сигнала и а является частным от деления амплитуды измеряемого сигнала на амплитуду контрольного сигнала, и значение квадратурной амплитуды этого же измеряемого сигнала, равное a⋅sinФ. Эти значения можно вычислять при помощи системы аффинных уравнений, имеющих для синфазной амплитуды и для квадратурной амплитуды коэффициенты, которые зависят от выбранных значений фазы контрольного сигнала.
Согласно первому возможному варианту выполнения вычислительного блока, он может осуществлять точное решение системы аффинных уравнений, в которых неизвестными являются значения синфазной а⋅cosФ и квадратурной a⋅sinФ амплитуд измеряемого сигнала. В этом случае вычислительный блок может быть выполнен с возможностью вычислять коэффициенты системы аффинных уравнений на основании выбранных значений фазы контрольного сигнала и вычислять значения синфазной и квадратурной амплитуд измеряемого сигнала с применением алгоритма решения этой системы аффинных уравнений. В частности, вычислительный блок может применять алгоритм инверсии аффинных уравнений или алгоритм решения при помощи наименьших квадратов, чтобы решить систему аффинных уравнений, в которой неизвестными являются синфазные и квадратурные амплитуды измеряемого сигнала.
Согласно второму возможному варианту выполнения вычислительного блока, он может осуществлять в первую очередь, в зависимости от амплитуды измеряемого сигнала, решение системы аффинных уравнений, в которой неизвестными являются значения синфазной а⋅cosФ и квадратурной a⋅sinФ амплитуд измеряемого сигнала. Такой метод применяют, когда амплитуда измеряемого сигнала намного меньше, чем амплитуда контрольного сигнала. В этом случае вычислительный блок может быть выполнен с возможностью определять приближенные значения коэффициентов синфазной амплитуды и квадратурной амплитуды в системе аффинных уравнений, причем эти приближенные значения коэффициентов не зависят от выбранных значений фазы измеряемого сигнала, и выбранные значения фазы контрольного сигнала образуют аффинные члены системы аффинных уравнений. В этом случае вычислительный блок может быть также выполнен с возможностью вычислять приближенные значения синфазной и квадратурной амплитуд измеряемого сигнала как простые линейные комбинации выбранных значений фазы контрольного сигнала.
Согласно третьему возможному варианту выполнения вычислительного блока, он может осуществлять решение системы аффинных уравнений, разбивая значения фазы контрольного сигнала, выбранные сдвиговым регистром, на основные и гармонические составляющие. В частности, вычислительный блок может быть выполнен с возможностью вычислять амплитуды синфазной и квадратурной основных составляющих и гармонических составляющих для выбранных значений фазы контрольного сигнала. В этом случае вычислительный блок может быть также выполнен с возможностью вычислять приближенные значения синфазной а⋅cosФ и квадратурной a⋅sinФ амплитуд измеряемого сигнала на основании линейных комбинаций амплитуд синфазной и квадратурной основных составляющих и гармонических составляющих выбранных значений фазы контрольного сигнала.
Предпочтительно, если используют третий вариант вычислительного блока, вычислительный блок может быть выполнен с возможностью вычислять приближенные значения амплитуд синфазной и квадратурной основных составляющих и гармонических составляющих выбранных значений фазы контрольного сигнала как комбинации сложений и вычитаний выбранных значений фазы контрольного сигнала. При этом он может быть также выполнен с возможностью вычислять приближенные значения синфазной а⋅cosФ и квадратурной a⋅sinФ амплитуд измеряемого сигнала на основании линейных комбинаций приближенных значений амплитуд синфазной и квадратурной основных составляющих и гармонических составляющих выбранных значений фазы контрольного сигнала. В этом случае число Р предпочтительно является кратным 60.
Если необходимо одновременно и постоянно характеризовать несколько синусоидальных сигналов, для каждого из этих сигналов может быть выделен отдельный канал считывания, но блок синтеза может общим для всех каналов считывания, чтобы выдавать в каждый из них контрольный сигнал и моментальные значения его фазы. Таким образом, такая система, которая выполнена с возможностью выдавать значения амплитуды и фазовой задержки, относящиеся к нескольким измеряемым сигналам, каждый из которых имеет синусоидальные изменения в зависимости от времени и все имеют частоту F, может содержать каналы считывания, которые выделены соответственно и индивидуально для измеряемых сигналов, при этом каждый канал считывания содержит компаратор и сдвиговый регистр, выполненные и подсоединенные, как было указано выше, отдельно от других каналов считывания. В этом случае блок синтеза может быть общим для всех каналов считывания, чтобы передавать контрольный сигнал одновременно во все компараторы и чтобы передавать моментальные значения фазы контрольного сигнала одновременно во все сдвиговые регистры. Вычислительный блок тоже может быть общим для всех каналов считывания, чтобы определять значение амплитуды и значение задержки отдельно для каждого измеряемого сигнала, для которого выделен один из каналов считывания.
В частных вариантах выполнения изобретения система может содержать:
- вход для приема сигнала тактового генератора;
- первый циклический накопитель, выполненный с возможностью генерировать фазу сигнала возбуждения на основании сигнала тактового генератора в соответствии с первым инкрементом накопления;
- второй циклический накопитель, выполненный с возможностью генерировать фазу контрольного сигнала на основании сигнала тактового генератора в соответствии с вторым инкрементом накопления;
- первый блок формирования сигнала для производства сигнала возбуждения с синусоидальной формой временных изменений на основании фазы, генерируемой первым циклическим накопителем; и
- второй блок формирования сигнала для производства контрольного сигнала на основании фазы, генерируемой вторым циклическим накопителем.
Система может быть также выполнена с возможностью выдавать сигнал возбуждения во внешнее устройство и с возможностью принимать измеряемый сигнал как реакцию этого внешнего устройства на сигнал возбуждения. Для этого первый и второй инкременты накопления являются положительными целыми числами, при которых частное от деления первого инкремента накопления на Q равно частному от деления второго инкремента накопления на Р, а также равно положительному целому числу, называемому инкрементом цикла. Таким образом, частота F может быть равна первому произведению частоты сигнала тактового генератора на число Q и на инкремент цикла, поделенный на 2NA, где NA является числом бит, используемых в каждом циклическом накопителе, и контрольная частота Fref может быть равна второму произведению частоты сигнала тактового генератора на число Р и на инкремент цикла, поделенный на 2NA.
Выход второго циклического накопителя подсоединен на входе к сдвиговому регистру каждого канала считывания для передачи моментальных значений фазы контрольного сигнала, и выход второго блока формирования сигнала одновременно подсоединен на входе к компаратору каждого канала считывания для передачи самого контрольного сигнала.
Вторым объектом изобретения является способ определения значения амплитуды и значения фазовой задержки, относящихся к измеряемому сигналу, который имеет синусоидальные изменения в зависимости от времени с частотой F. Этот способ содержит следующие этапы:
- генерируют контрольный сигнал, который имеет синусоидальную форму временных изменений, находящуюся в постоянной фазовой взаимосвязи с измеряемым сигналом, причем этот контрольный сигнал имеет амплитуду, большую, чем амплитуда измеряемого сигнала, и имеет частоту, равную Fref = F x P/Q, где P и Q являются двумя фиксированными не равными нулю положительными целыми числами, при этом Р больше, чем Q,
- выбирают моментальные значения фазы контрольного сигнала, при которых измеряемый сигнал становится меньше, чем контрольный сигнал, или при которых измеряемый сигнал становится больше, чем контрольный сигнал;
- вычисляют значения амплитуды и фазовой задержки измеряемого сигнала на основании выбранных значений фазы контрольного сигнала.
Такой способ можно осуществлять, используя систему, являющуюся первым объектом изобретения.
Предпочтительно заявленный способ можно применять, чтобы характеризовать реакцию резонатора, который начинает вибрировать под действием сигнала возбуждения, имеющего синусоидальную форму временных изменений с частотой F. При этом измеряемый сигнал представляет собой реакцию резонатора на сигнал возбуждения. В частности, резонатор может входить в состав виброакселерометра или виброгироскопа, и значения амплитуды и фазовой задержки, относящиеся к измеряемому сигналу, используют затем для вычисления значений ускорения или скорости вращения прибора или транспортного средства, на котором установлен акселерометр или гироскоп.
Другие отличительные признаки и преимущества настоящего изобретения будут более очевидны из нижеследующего описания не ограничительных примеров выполнения со ссылками на прилагаемые чертежи, на которых:
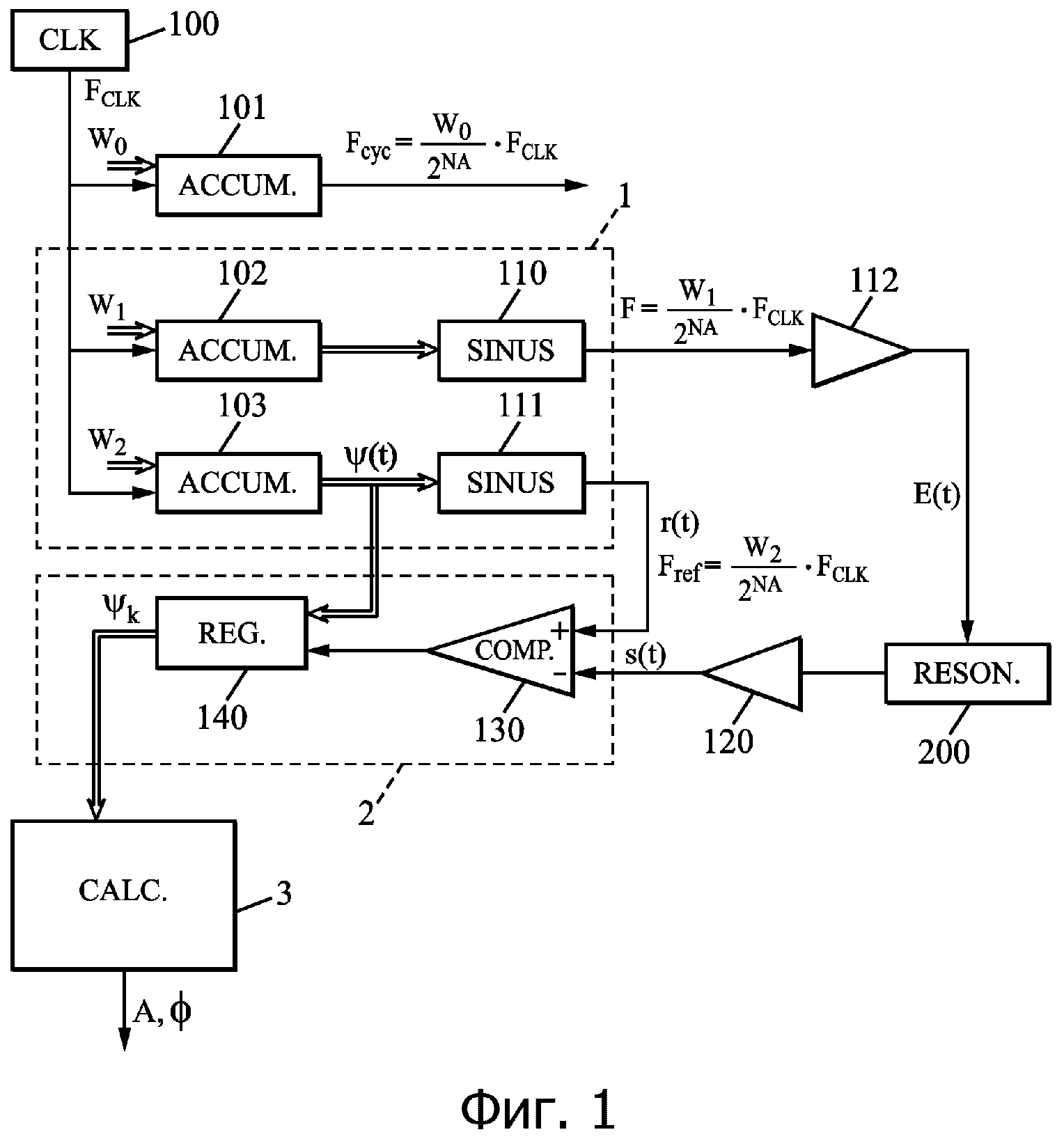
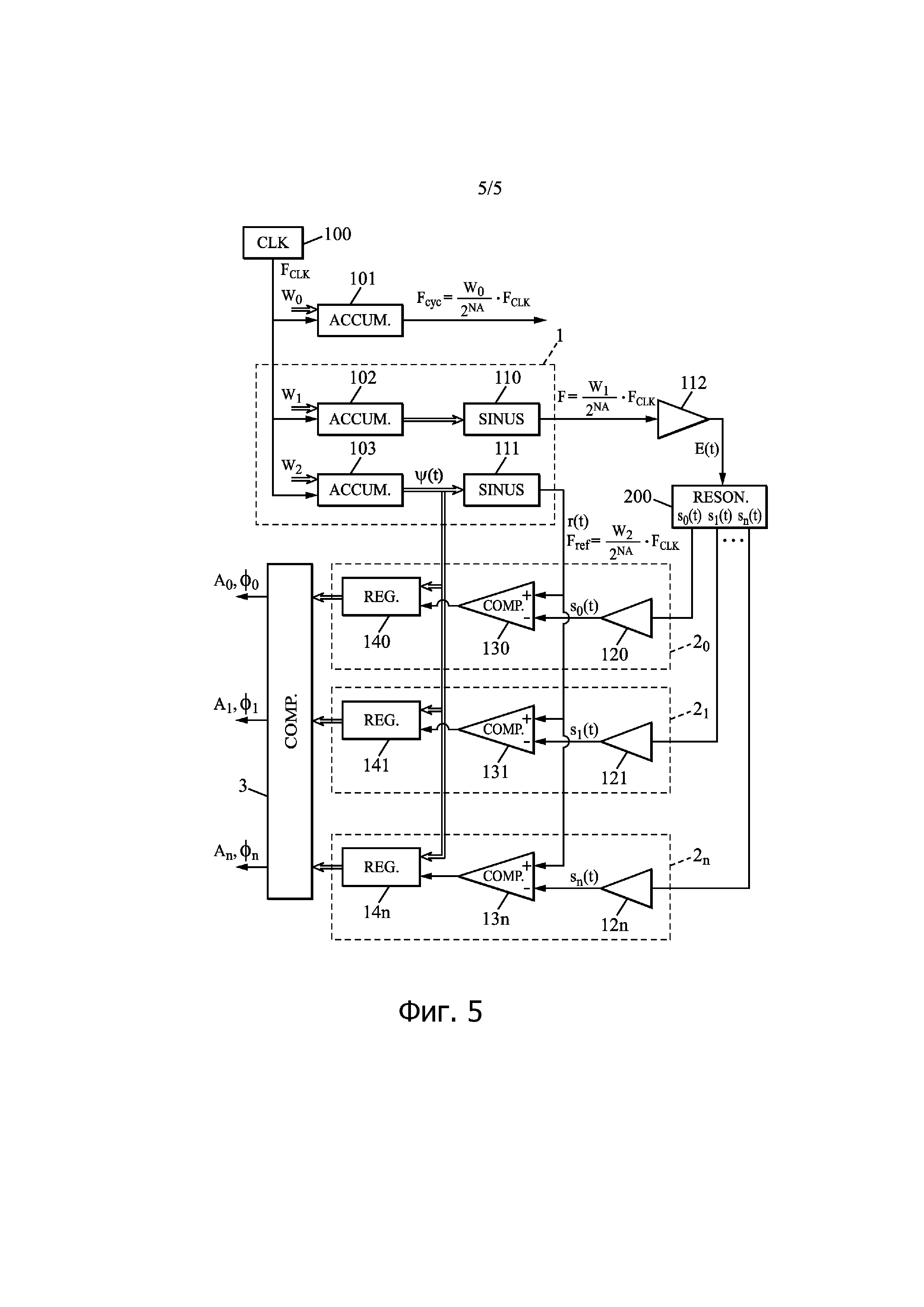
Фиг. 1 - структурная схема заявленной системы.
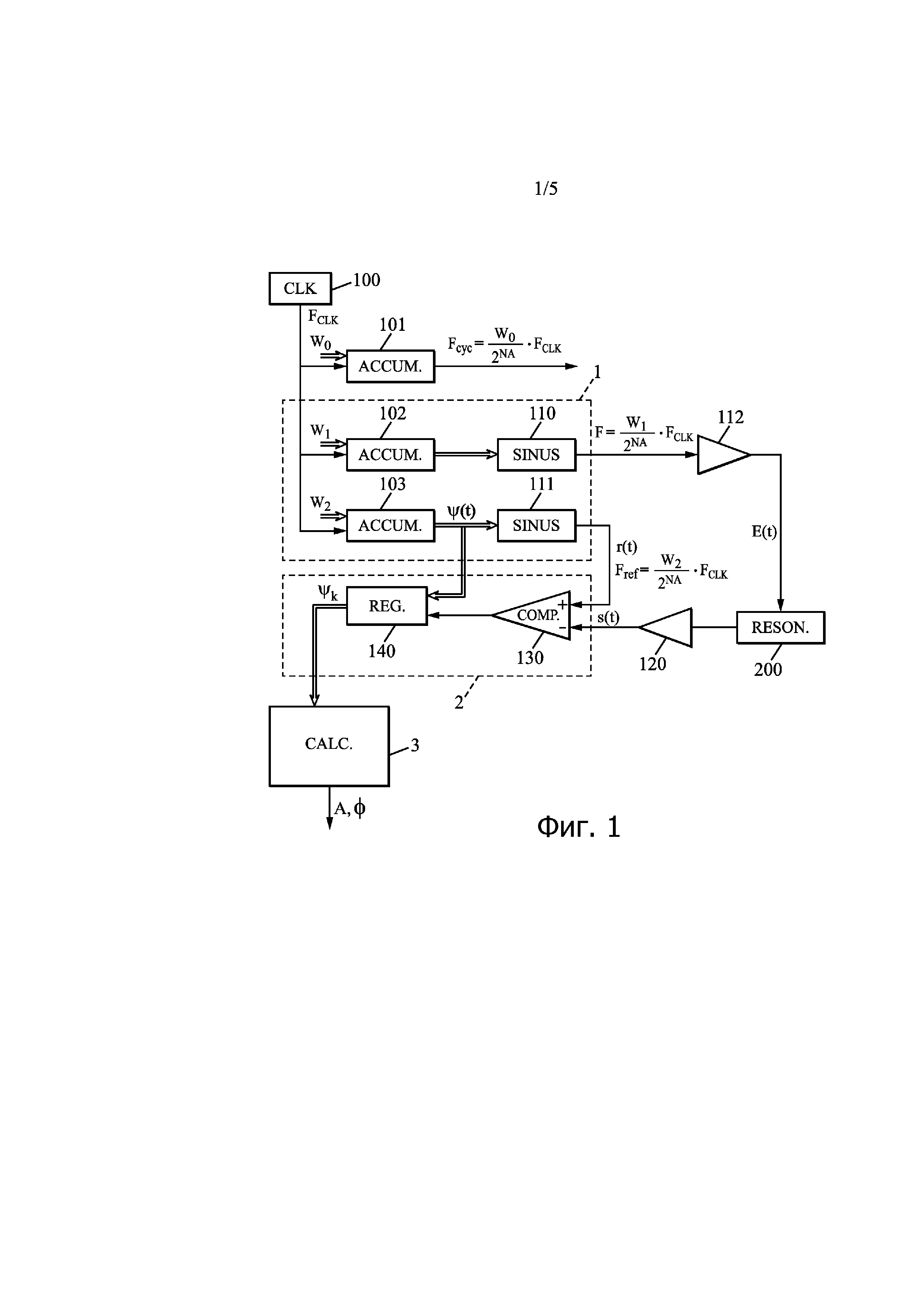
Фиг. 2 - временная диаграмма, на которой показаны значения фазы, выбранные заявленной системой.
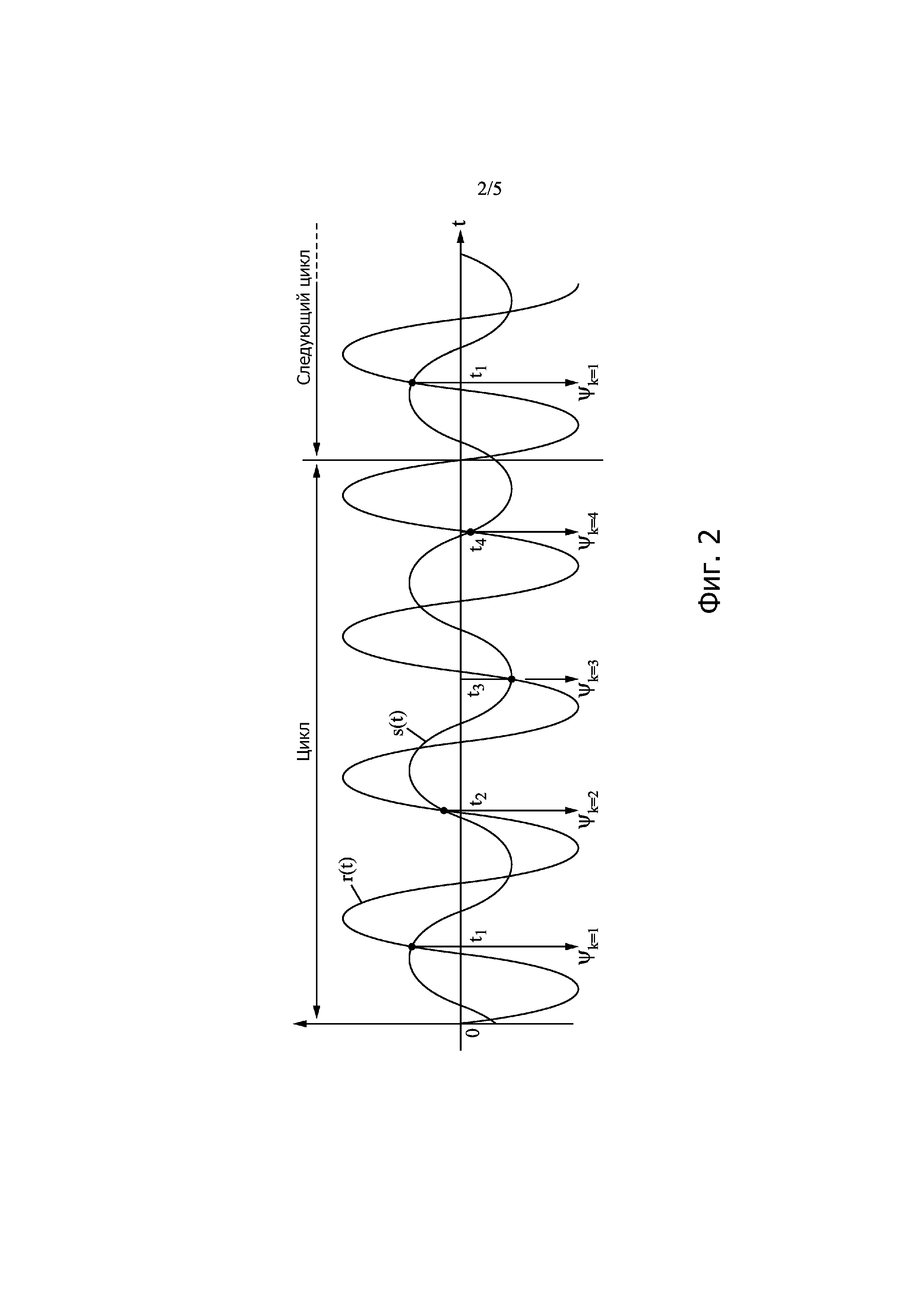
Фиг. 3а-3с - три вида системы аффинных уравнений, неизвестными в которых являются синфазные и квадратурные амплитуды измеряемого сигнала.
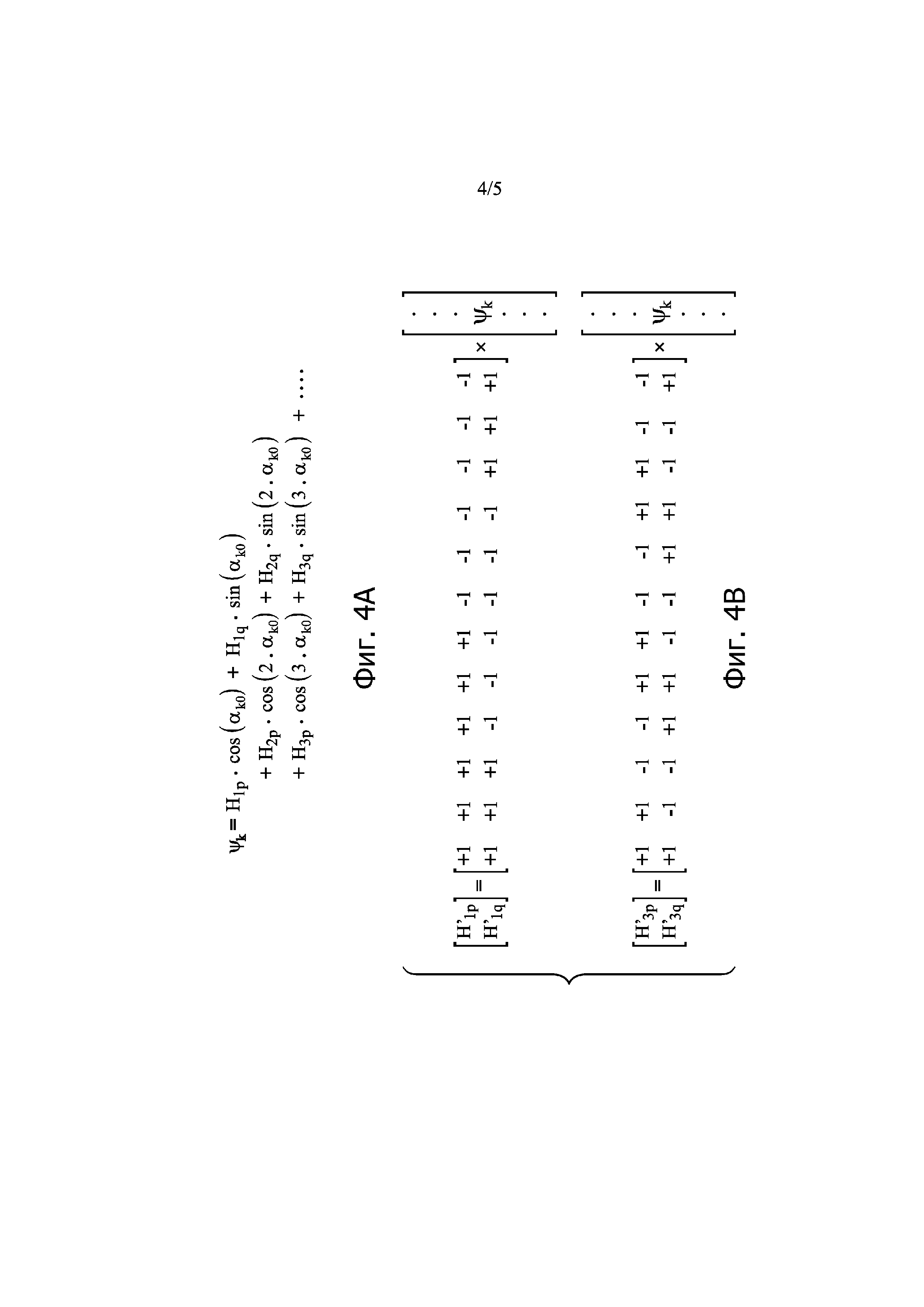
Фиг. 4а - разложение в ряд Фурье значений фазы, используемых в рамках изобретения.
Фиг. 4b - вычисление приближенных значений для коэффициентов Фурье значений фазы, используемых в рамках изобретения.
Фиг. 5 соответствует фиг. 1 для усовершенствованного варианта изобретения, который предназначен для нескольких одновременно измеряемых сигналов.
На фиг. 1 и 5 двойными стрелками показаны передачи двоичных слов, а простыми стрелками показаны передачи аналоговых сигналов.
Заявленная система предназначена для характеризации синусоидального сигнала, называемого измеряемым сигналом и обозначаемого s(t), частота временного изменения которого предположительно известна. Этот измеряемый сигнал имеет, таким образом, форму:
s(t) = A·sin(2π·F·t – Φ) (1)
где t обозначает время, F является известной частотой сигнала s(t), и A и Φ являются соответственно амплитудой и фазовой задержкой сигнала s(t). Таким образом, задачей изобретения является определение значений амплитуды А и фазовой задержки Ф.
Для этого в рамках изобретения применяют другой синусоидальный сигнал, называемый контрольным сигналом и обозначаемый r(t), который полностью известен и генерирован таким образом, чтобы находиться в постоянной фазовой взаимосвязи с измеряемым сигналом s(t). Под постоянной фазовой взаимосвязью между сигналами s(t) и r(t) следует понимать свойство этих сигналов, которое состоит в том, что каждый из них меняется по своей соответствующей частоте с учетом фазового сдвига, который первоначально существует между обоими сигналами. Иначе говоря, каждый сигнал обладает частотной стабильностью, при которой он сохраняет, по меньшей мере в течение времени, необходимого для характеризации измеряемого сигнала s(t), фиксированное значение для своей собственной фазовой задержки. Выбирая соответствующим образом первоначальный момент, определяемый как t=0, можно записать контрольный сигнал как:
r(t) = - Aref·sin(2π·Fref·t) (2)
Иначе говоря, первоначальный момент t=0 определяют таким образом, чтобы контрольный сигнал r(t) имел фазовую задержку, равную π. Aref и Fref соответственно являются амплитудой и частотой временного изменения контрольного сигнала r(t), которые считаются известными. В дальнейшем фаза контрольного сигнала r(t) будет обозначаться ψ(t): ψ(t) = 2π·Fref·t.
Как показано на фиг. 1, контрольный сигнал r(t) генерируется блоком 1 синтеза. Согласно возможному варианту выполнения блока 1 синтеза, который является предпочтительным для изобретения, он может содержать циклический накопитель 103, называемый в общей части этого описания вторым циклическим накопителем и обозначенный ACCUM, который принимает на входе периодический сигнал, выдаваемый тактовым генератором 100, обозначенным CLK. Тактовый генератор 100 может быть внешним относительно блока 1 синтеза и, в частности, может использоваться другими системами или электронными модулями, внешними по отношению к заявленной системе. На выходе циклический накопитель 103 производит линейно нарастающую функцию, которая переустанавливается автоматически, на частоте Fref = FCLK·W2/2NA, где FCLK является частотой тактового генератора 100, W2 является фиксированным инкрементом накопления, и NA является числом бит, используемых для циклического накопителя. Блок 111 формирования сигнала, обозначенный SINUS, преобразует линейно нарастающую функцию, производимую циклическом накопителем 103, в синусоидальный сигнал тоже на частоте Fref. Как известно, блок 111 формирования сигнала может быть выполнен в виде цифровой таблицы преобразования (“lookup table” на английском языке), которую комбинируют с цифро-аналоговым преобразователем, или в виде фильтрующего трансформатора, и т.д. Сигнал, производимый блоком 111, является контрольным сигналом r(t), а сигнал, генерируемый циклическим накопителем 103, является фазой этого контрольного сигнала r(t), обозначенной ψ(t), где t обозначает время.
По сути дела, для многих вариантов применения изобретения измеряемый сигнал s(t) является ответом резонатора 200, обозначенного RESON и еще называемого часто принудительным генератором колебаний, на сигнал возбуждения. Следовательно, этот сигнал возбуждения, обозначенный E(t), имеет ту же частоту F, что и измеряемый сигнал s(t). Естественно, сигнал возбуждения E(t) и измеряемый сигнал s(t) находятся в постоянной фазовой взаимосвязи друг с другом, и в этом случае необходимо обеспечивать, чтобы сигнал возбуждения E(t) и контрольный сигнал r(t) тоже были в постоянной фазовой взаимосвязи друг с другом. Наиболее предпочтительный способ обеспечения такой постоянной фазовой взаимосвязи между сигналом возбуждения E(t) и контрольным сигналом r(t) состоит в генерировании последнего тоже при помощи блока 1 синтеза. Для этого блок 1 синтеза может также содержать другой циклический накопитель 102, называемый в общей части этого описания первым циклическим накопителем, который тоже принимает на входе периодический сигнал, выдаваемый тактовым генератором 100. На выходе циклический накопитель 102 производит другую линейно нарастающую функцию, которая переустанавливается автоматически, на частоте F = FCLK·W1/2NA, где W1 является другим фиксированным инкрементом накопления. В общей части настоящего описания W1 и W2 соответственно называются первым и вторым инкрементами накопления.
Блок 110 формирования сигнала преобразует линейно нарастающую функцию, производимую циклическим накопителем 102, в другой синусоидальный сигнал, который имеет частоту F. Этот блок 110 формирования сигнала тоже может быть выполнен в виде цифровой таблицы преобразования, которую комбинируют с цифро-аналоговым преобразователем, или в виде фильтрующего трансформатора, и т.д. Сигнал, производимый блоком 110 и затем, возможно, усиливаемый усилителем 112, является сигналом возбуждения E(t).
Инкременты накопления W1 и W2 являются положительными целыми числами, выбираемыми таким образом, чтобы W1/Q = W2/P = W0, где P и Q являются двумя не равными нулю фиксированными положительными целыми числами, при этом P больше, чем Q. Таким образом: Fref = FCLK·(P·W0)/2NA, F = FCLK·(Q·W0)/2NA, и, следовательно, Fref = F·P/Q. Следовательно, частота Fref контрольного сигнала r(t) больше частоты F измеряемого сигнала s(t). Например, частота FCLK тактового генератора может быть равна 300 МГц, и число NA бит, используемых в циклических накопителях 102 и 103, может составлять 32. В этом случае отношение Fref к FCLK может составлять, например, около 1/1000.
Кроме того, числа Р и Q предпочтительно можно выбирать таким образом, чтобы W0 тоже было положительным целым числом, называемым инкрементом цикла. В этом случае блок 1 синтеза может содержать еще один циклический накопитель, обозначенный позицией 101 на фиг. 1, который тоже принимает сигнал тактового генератора на частоте FCLK и который имеет инкремент цикла W0 в качестве инкремента накопления. Таким образом, циклический накопитель 101 производит на выходе линейно нарастающую функцию, которую периодически переустанавливают на частоте Fcyc = FCLK·W0/2NA. Таким образом, Fref = Fcyc·P, и F = Fcyc·Q: временной период контрольного сигнала r(t) в Р раз короче, чем временной период сигнала, производимого циклическим накопителем 101, и временной период измеряемого сигнала s(t) в Q раз короче, чем временной период сигнала, производимого циклическим накопителем 101. Таким образом, этот накопитель выдает сигнал синхронизации цикла.
Измеряемый сигнал s(t) поступает от резонатора 200, возможно, через усилитель 120. Примеры резонатора 200 будут приведены ниже в конце настоящего описания. Измеряемый сигнал s(t) обрабатывается в канале 2 считывания, затем в вычислительном блоке 3, обозначенном CALC. В качестве результатов последний выдает цифровые значения для амплитуды А и для фазовой задержки Ф измеряемого сигнала s(t).
Канал 2 считывания содержит компаратор 130, обозначенный СОМР, и сдвиговый регистр 140, обозначенный REG. Компаратор 130 принимает на двух отдельных входах контрольный сигнал r(t) и измеряемый сигнал s(t). На выходе он выдает сигнал сравнения, которые имеет переходы каждый раз, когда контрольный сигнал r(t) становится больше, чем измеряемый сигнал s(t). Хотя в дальнейшем настоящее описание относится к этой работе компаратора 130, эквивалентную работу можно получить с компаратором, который производит переходы в сигнале сравнения каждый раз, когда измеряемый сигнал s(t) становится больше, чем контрольный сигнал r(t). Затем сигнал сравнения поступает в сдвиговый регистр 140, который одновременно принимает на отдельном входе моментальное значение фазы ψ(t) контрольного сигнала r(t) от циклического накопителя 103. Сдвиговый регистр 140 передает на выходе последовательно значения фазы ψ(t) в моменты, когда контрольный сигнал r(t) становится больше измеряемого сигнала s(t). Эти значения, обозначенные ψk и пронумерованные целыми числами k, начиная с 1, передаются затем в вычислительный блок 3.
Вычислительный блок 3 предпочтительно выполнен в виде специальной схемы или ASIC, или в виде программируемой логической схемы или FPGA. В варианте эта схема ASIC или эта схема FPGA могут выполнять функции компаратора 130 и сдвигового регистра 140.
На фиг. 2 представлена временная диаграмма сигналов r(t) и s(t). На ней показаны моменты t1, t2, t3,…, tk,…, в которые контрольный сигнал r(t) становится больше измеряемого сигнала s(t). Соответствующими значениями фазы ψ(t) контрольного сигнала r(t) соответственно являются ψk=1 = ψ(t1), обозначаемое в дальнейшем ψ1, ψk=2 = ψ(t2), обозначаемое ψ2, ψk=3 = ψ(t3), обозначаемое ψ3,…, ψk = ψ(tk),… Индекс k отсчитывает, таким образом, последовательные периоды контрольного сигнала r(t), начиная от первоначального момента t=0. Две последовательности амплитуд и значений фазы ψk в точках пересечения между кривыми сигналов r(t) и s(t) являются периодическими с продолжительностью периода, равной 1/Fcyc. Эта продолжительность периода определяет цикл считывания значений фазы ψk, который является надлежащим для применения изобретения. При этом последовательные циклы считывания могут управляться сигналом, который генерирует вышеупомянутый циклический накопитель 101, и индекс k меняется от 1 до Р в ходе каждого цикла считывания с индивидуальной продолжительностью 1/Fcyc.
Как правило, в рамках изобретения число Р может быть равно числу Q, увеличенному на единицу: P = Q + 1. Например, Q можно выбрать равным 3, а Р можно выбрать равным 4. Фиг. 3 соответствует этим значениям Р и Q, и на ней показан полный цикл считывания с началом следующего цикла.
Уравнениями, которым отвечают моменты tk, являются s(tk) = r(tk), то есть:
A·sin[2π·(Q/P)·Fref·tk – Φ] = - Aref·sin(2π·Fref·tk) (3)
В соответствии с работой канала 2 считывания:
2π·Fref·tk = ψk + 2·kπ - π (4)
При этом для каждого значения k уравнения (3) принимают вид:
A·sin[(Q/P)·(ψk + (2k-1)π) – Φ] = Aref·sin(ψk) (5)
Если обозначить a=A/Aref и αk0 = (Q/P)·(2k-1)π, то уравнениями, которым удовлетворяют значения фазы ψk, являются, как показано на фиг. 3а:
a·sin[αk0 + (Q/P)·ψk – Φ] = sin(ψk) (6)
Значение Aref амплитуды контрольного сигнала r(t) сохраняют в памяти, чтобы его мог в дальнейшем использовать вычислительный блок 3. Развернув синус первого члена, получаем:
a·sin[αk0 + (Q/P)·ψk]·cos(Φ) - a·cos[αk0 + (Q/P)·ψk]·sin(Φ) = sin(ψk) (7)
При этом осуществляют следующее изменение переменных, при котором вводят синфазную амплитуду Х и квадратурную амплитуду Y измеряемого сигнала s(t):
X = a·cos(Φ) (8a)
Y = a·sin(Φ) (8b)
Для каждого значения k в зависимости от новых неизвестных Х и Y, которые заменяют Aref и Ф в первой фазе решения, уравнения (7) становятся:
sin[αk0 + (Q/P)·ψk] · X – cos[αk0 + (Q/P)·ψk] · Y = sin(ψk) (9)
что соответствует матричной записи на фиг. 3b.
Решение системы уравнений (9) дает значения синфазной Х и квадратурной Y амплитуд измеряемого сигнала s(t). На основании этих значений для Х и Y уравнения (8а) и (8b) дают значения а и фазовой задержки Ф, например, а = (X2 + Y2)1/2 и Φ = Arctan(Y/X), затем амплитуду А измеряемого сигнала s(t) вычисляют как произведение a·Aref. Следовательно, в дальнейшем настоящее описание будет сфокусировано на решении системы уравнений (9), соответствующей фиг. 3b, с предложением нескольких альтернативных методов для этого решения, которые может применять вычислительный блок 3: метод точного решения, метод приближенного решения, метод решения посредством разложения в ряд Фурье значений фазы ψk.
Точное решение:
Система уравнений (9), соответствующая матричной записи, показанной на фиг. 3b, с двумя амплитудами Х и Y в качестве неизвестных, является системой аффинных уравнений, коэффициенты в которых зависят от значений фазы ψk, которые были получены через канал 2 считывания. Эти коэффициенты sin[αk0 + (Q/P)·ψk] и -cos[αk0 + (Q/P)·ψk] для каждого значения k, соответствующего отдельному уравнению, вычисляются вычислительным блоком 3, затем систему можно точно решить при помощи одного из методов, известных специалисту в данной области: обращение матрицы системы, образованной двумя из уравнений (9), или решение при помощи метода наименьших квадратов, и т.д. Если используют метод посредством обращения матрицы, вычисляют матрицу 2х2 коэффициентов Х и Y в двух из уравнений (9), затем производят ее обращение, и обратную матрицу применяют к вторым членам sin(ψk) обоих используемых уравнений (9), чтобы получить значения Х и Y. Вместе с тем, метод решения при помощи наименьших квадратов является более точным, так как он использует все уравнения (9).
Кроме того, поскольку коэффициенты sin[αk0 + (Q/P)·ψk] и -cos[αk0 + (Q/P)·ψk] являются переменными в зависимости от значений фазы ψk, которые были получены через канал 2 считывания, то вычисления значений синуса и косинуса, которые образуют коэффициенты Х и Y в уравнениях (9), могут занимать много времени и много вычислительных ресурсов. В этом случае можно заменить функции синуса и косинуса их ограниченными разложениями, предпочтительно по меньшей мере до пятого порядка, чтобы ограничить вытекающие из них погрешности на значениях Х и Y.
Приближенное решение при малых значениях а:
Этот метод можно применять, когда амплитуду Aref контрольного сигнала r(t) регулируют таким образом, чтобы она была намного больше, чем амплитуда А измеряемого сигнала s(t). Иначе говоря: a<<1, и в соответствии с уравнением (6) значения фазы ψk являются намного меньшими, чем π, и, следовательно, намного меньшими значений αk0. В этих условиях уравнения (6) принимают следующий вид:
a·sin(αk0 – Φ) ≈ ψk (10)
то есть в зависимости от неизвестных Х и Y:
X · sin(αk0) – Y · cos(αk0) ≈ ψk (11)
что соответствует матричной записи на фиг. 3с.
На этот раз коэффициенты sin(αk0) и -cos(αk0) соответственно для Х и Y в системе аффинных уравнений (11) являются постоянными. Следовательно, их можно рассчитать заранее. Можно также заранее произвести обращение матрицы 2х2 системы, образованной любыми двумя уравнениями из уравнений (11), и обратную матрицу можно сохранить в памяти для ее непосредственного использования вычислительным блоком 3. При этом значения амплитуд Х и Y можно вычислить просто, применив эту обратную матрицу к вторым членам ψk двух используемых уравнений (11). Такую предварительную запись обратной матрицы можно также применить для метода решения при помощи наименьших квадратов.
Метод посредством разложения в ряд Фурье
Как было указано выше, последовательность значений фазы ψk является периодической с временным периодом 1/Fcyc. Это же относится и к последовательным значениям αk0. При этом ставится задача решения системы уравнений (9), выразив значения фазы ψk в виде линейной комбинации sin(αk0), cos(αk0), sin(2·αk0), cos(2·αk0), sin(3·αk0), cos(3·αk0), … то есть:
ψk = Σi=1, 2, 3,…, P [Hip · cos(i·αk0) + Hiq · sin(i·αk0) (12)
что соответствует развернутой записи на фиг. 4а. Эта запись представляет собой разложение значений фазы ψkв ряд Фурье на основе значений αk0. Таким образом, H1p является амплитудой синфазной основной составляющей, H1q является амплитудой квадратурной основной составляющей значений ψk, и коэффициенты Hip и Hiq при i, превышающем 1, являются амплитудами гармонических составляющих порядка i.
Однако уравнение (9) можно записать как:
[X·sin(αk0) - Y·cos(αk0)]·cos((Q/P)·ψk)
+ [X·cos(αk0) + Y·sin(αk0)]·sin((Q/P)·ψk) - sin(ψk) = 0 (13)
Развернув cos((Q/P)·ψk), sin((Q/P)·ψk) и sin(ψk) в ряд Фурье (Q/P)·ψk и ψk и применив к ним выражение (12) для ψk, затем преобразовав все члены вида sinn(i·αk0) и cosn(i·αk0) в линейные комбинации членов вида sin(n’·i·αk0) и cos(n’·i·αk0), получают нулевую линейную комбинацию членов sin(n·i·αk0) и cos(n·i·αk0).. Следовательно, каждый из множителей этой линейной комбинации должен быть нулевым, что дает систему аффинных уравнений, неизвестными в которой являются коэффициенты Hip и Hiq, при этом i обозначает совокупность не равных нулю натуральных целых чисел, меньших или равных Р. Полученными таким образом первыми коэффициентами разложения ψk в ряд Фурье являются:
H1p = X + [(P2 - Q2)/(8P2)]·X3 + [(P2 - Q2)/(8P2)]·X·Y2 + член в X4 + … (14a)
H2p = (Q/2P)·X2 + член в X4 + … (14b)
H3p = [(P2 - 9Q2)/(24P2)]·X3 + [(P2 - 9Q2)/(8P2)]·X·Y2 + член в X4 + … (14c)
H4p = [(P2Q - 4Q3)/(2P3)]·X2·Y2 + член в X4 + … (14d)
H5p = -[(9P4 - 250P2Q2 + 625Q4)·Y2/(192P4)]·X3 + term in X5 (14e)
…
H1q = Y + [(P2 - Q2)/(8P2)]·X2·Y + член в Y3 + … (14f)
H2q = (Q·X/P)·Y + член в Y3 + … (14g)
H3q = [(-P2 + 9Q2)/(8P2)]·X2·Y + член в Y3 + … (14h)
…
Кроме того, коэффициенты Hip и Hiq разложения в ряд Фурье можно вычислить обычным путем на основании значений фазы ψk, поступающих от канала 2 считывания. Вместе с тем, можно вычислить приближенные значения коэффициентов H1p и H1q, обозначаемые H’1p и H’1q, быстрее, применив первое матричное отношение, показанное на фиг. 4b, к значениям фазы ψk (данный пример с Р, равным 12). Затем вычисленные таким образом значения H’1p и H’1q используют непосредственно как значения H1p и H1q. Чтобы вычислить в тех же простых условиях коэффициенты гармонических амплитуд порядка 3 и 5, необходимо, чтобы число Р было также кратным 3 или 5 в дополнение к тому, что оно является кратным 4, при упрощенных вычислениях H1p, H1q и H2p, H2q, а также H4p, H4q. Для применения таких вычислительных упрощений предпочтительно Р должно быть кратным 60. Когда число Р к тому же равно 12, второе матричное отношение на фиг. 4b показывает вычисление приближенных значений коэффициентов H3p и H3q, обозначенных H’3p и H’3q.
Идентифицируя первые коэффициенты Hip и Hiq разложения в ряд Фурье значений фазы ψk, вычисленных на основании значений, выданным каналом 2 считывания, с выражениями уравнений (14а-14h), можно приближенно получить амплитуды Х и Y, комбинируя несколько из уравнений (14а-14h) следующим образом:
X ≈ H1p + 3·H3p·(P2 - Q2)/(P2 - 9·Q2) + H5p·(P2 - Q2)/(P2 - 25·Q2) (15a)
Y ≈ H1q - H3q·(P2 - Q2)/(P2 - 9·Q2) (15b)
Так, приближенное значение Х можно вычислить, комбинируя линейно вместе с коэффициентами комбинации, которые являются фиксированными и определены заранее, значения только трех амплитуд составляющих Фурье H1p, H3p и H5p. Параллельно можно вычислить приближенное значение Y, просто комбинируя значения только двух амплитуд составляющих Фурье H1q и H3q. Для комбинаций уравнений (15a-15b) первые пренебрегаемые члены находятся в X·Y2. Альтернативно можно использовать другие комбинации для вычисления приближенных значений амплитуд Х и Y, пренебрегая членами в X3 вместо членов в X·Y2.
Следует отметить, что можно сделать максимальным значение синфазной амплитуды Х измеряемого сигнала s(t) по сравнению с квадратурной амплитудой Y, изначально применяя вращение между Р значениями фазы ψk. Такое вращение соответствует смещению первоначального момента t=0 для уменьшения фазовой задержки Ф. Это позволяет минимизировать остаточные перекрестные члены по X·Y2 в Hip.
Фиг. 5 соответствует фиг. 1, когда резонатор 200 или эквивалентно набор резонаторов, обозначенный 200, выдает одновременно несколько ответов на единый сигнал возбуждения E(t). Это относится, например, к случаю, когда резонатор или набор резонаторов 200 входит в состав виброакселерометра или виброгироскопа. Каждый измеряемый сигнал, обозначаемый s0(t), s1(t),…, sn(t), представляет собой отдельную реакцию на единый сигнал возбуждения E(t), и для каждого из этих измеряемых сигналов выделен отдельный канал считывания. Так, канал считывания 20, содержащий компаратор 130 и сдвиговый регистр 140, а также, возможно, усилитель 120, выделен для измеряемого сигнала s0(t). Точно так же, канал считывания 21, содержащий компаратор 131 и сдвиговый регистр 141, а также, возможно, усилитель 121, выделен для измеряемого сигнала s1(t),…, канал считывания 2n, содержащий компаратор 13n и сдвиговый регистр 14n, а также, возможно, усилитель 12n, выделен для измеряемого сигнала sn(t). Параллельно компараторы 130, 131,…, 13n получают контрольный сигнал r(t) от блока 111 формирования сигнала, а сдвиговые регистры 140, 141, 14n получают параллельно фазу ψ(t) контрольного сигнала r(t) от циклического накопителя 103. Таким образом, блок 1 синтеза является общим для всех каналов 20, 21, ..., 2n считывания. Вычислительный блок 3 тоже может быть общим для всех каналов 20, 21, ..., 2n считывания, например, работая поочередно в последовательные периоды считывания на основании значений фазы, которые поступают от одного или другого из каналов считывания. Таким образом, блок 3 определяет значения амплитуды и фазовой задержки всех измеряемых сигналов: A0 и Φ0 для измеряемого сигнала s0(t), A1 и Φ1 для измеряемого сигнала s1(t),…, An и Φn для измеряемого сигнала sn(t).
Когда набор резонаторов 200 является акселерометром, он может состоять по меньшей мере из трех брусков, на каждый из которых может действовать напряжением инерционный груз, и которые могут быть ориентированы не так, как другие бруски, например, в трех перпендикулярных направлениях. Каждый брусок может приводиться в колебание поперечно сигналом возбуждения E(t), и измеряемые сигналы s1(t), s2(t) и s3(t) могут характеризовать моментальные перемещения при поперечных вибрациях, соответственно для трех брусков. Специалист в данной области может вывести три составляющие приводного ускорения на основании значений амплитуд и фазовых задержек A1 и Φ1, A2 и Φ2, и A3 и Φ3 соответственно измеряемых сигналов s1(t), s2(t) и s3(t).
Когда резонатор 200 является гироскопом, он может состоять из конструкции, вибрирующей по меньшей мере с четырьмя собственными модами вибрации, которые могут быть связаны через поле силы Кориолиса. В этом случае измеряемые сигналы s1(t), s2(t) и s3(t) могут характеризовать связи между одной собственной модой возбуждения и тремя другими собственными модами, которые связаны с собственной модой возбуждения через поле силы Кориолиса. К собственной моде возбуждения прикладывают сигнал возбуждения E(t), и сигналы моментальных перемещений, которые относятся к трем другим собственным модам вибрации, образуют три измеряемых сигнала s1(t), s2(t) и s3(t). Специалист в данной области может вывести три составляющие приводного вращения на основании значений амплитуд и фазовых задержек A1 и Φ1, A2 и Φ2, и A3 и Φ3 соответственно измеряемых сигналов s1(t), s2(t) и s3(t).
Приводное ускорение или приводное вращение, которое измеряют таким образом, может быть результатом, в частности, движения прибора или транспортного средства, на котором установлен акселерометр или гироскоп, такого как летательный аппарат, спутник, космический корабль и т.д.