Результат интеллектуальной деятельности: СПОСОБ НАХОЖДЕНИЯ СОПРЯЖЕННЫХ ВЕКТОРОВ НАПРАВЛЕНИЙ НА ДВИЖУЩИЕСЯ ОБЪЕКТЫ
Вид РИД
Изобретение
Изобретение относится к пассивным системам радиовидения миллиметрового диапазонов длин волн [1], предназначенным для наблюдения за малоразмерными движущимися объектами. При обнаружении объектов [1], определении дальностей до них и оценивании пространственных координат в пассивной системе двух и более наблюдателей первоочередной задачей является поиск сопряженных пар ортов векторов направлений на соответствующие объекты, если число этих объектов больше одного.
В оптических систем видимого и инфракрасного диапазонов длин волн орты направлений на объекты формируются прохождением лучей через фокусы оптических линз, которые отображаются в матрицах изображений практически мгновенно. Поэтому время получения изображений мало по сравнению с временем перемещения объектов в поле видимости.
Для радиометрической системы, состоящей из двух радиометров с синхронно сканирующими по пространству антеннами, орты направлений на объекты образуются линией визирования антенн и запоминаются в угловых координатах азимута и угла места элементов матриц радиоизображений (РИ). При известной скорости построчного сканирования вычисляются и запоминаются моменты времени формирования ортов. Для сопряженных ортов направлений на один и тот же объект моменты времени их образования в общем случае отличаются. Это объясняется как движением объектов, так и различной ориентацией систем координат радиометров.
Наряду с изображениями объектов в матрицах РИ присутствуют изображения ложных образований, обусловленных помехами, и соответственно имеются ложные орты случайных направлений. В связи с этим требуется разработка способа поиска сопряженных векторов направлений на объекты и определения их пространственных координат, учитывающего движение объектов и наличие случайных помех.
В качестве прототипа рассмотрим способ нахождения сопряженных пар векторов [2, с. 182-186] в системе двух наблюдателей, основанный на свойстве компланарных векторов. Применительно к радиометрической системе способ заключается в следующем.
1. Для двух радиометров, взаимно удаленных на базовое расстояние d0, формируются орты i-x и j-x направлений на объекты a(i), 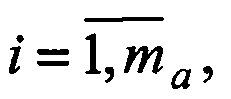 и b(j),
и b(j), 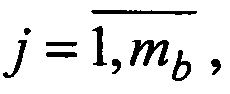 где ma и mb - число ортов в первом и втором радиометрах.
где ma и mb - число ортов в первом и втором радиометрах.
2. Рассматриваются i-e, j-е варианты соединения ортов в пары. Для каждого i-го, j-го варианта вычисляется показатель J(i, j) необходимого условия сопряжения:
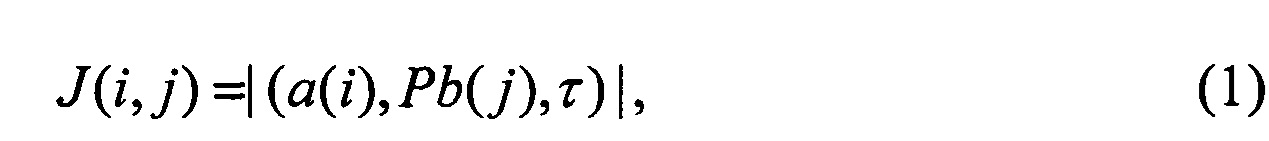
представляющий модуль смешанного произведения трех векторов: вектора a(i); вектора b'=Pb(j), где Р - матрица поворота осей координат при переходе в систему координат первого радиометра; τ - орт базового вектора d=d0τ, указывающего направление от первого радиометра ко второму.
3. Показатель (1) сравнивается с малым положительным числом ε. Если J(i, j)>ε, то данный вариант соединения ортов отвергается. Если J(i, j)≤ε, то i-й, j-й вариант считается правдоподобным, так как, если векторы а(i) и b(j) являются сопряженными (направлены на один и тот же объект), то указанные три вектора лежат в одной плоскости, и их смешанное произведение близко к нулю (с точностью до ошибок сопряжения).
4. Из всех пар соединения ортов выбираются 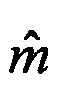 неповторяющихся пар с наименьшими значениями показателей (1).
неповторяющихся пар с наименьшими значениями показателей (1).
5. Для каждой выбранной пары сопряженных ортов а(i) и b(j) вычисляются оценки дальностей до соответствующего объекта ra(i) и rb(j), а также векторы оценок пространственных координат объекта Ma(i)=ra(i)a(i) и Mb(j)=rb(j)b(j) в системах координат двух радиометров.
Данный способ обладает следующими недостатками.
1. Способ не учитывает движение объекта на промежутке времени между двумя моментами ta(i) и tb(j), ta(i)≠tb(j), образования ортов а(i) и b(j), из-за чего нарушается условие компланарности векторов..
2. Близость показателя (1) к нулю не всегда означает сопряжение векторов а(i) и b(j), то есть принадлежность одному объекту, так как в одной плоскости могут лежать векторы, не принадлежащие одному объекту. Поэтому требуется дополнительная проверка на достаточность сопряжения.
Заявляемое техническое решение направлено на устранение этих недостатков.
Технический результат предлагаемого технического решения достигается применением способа нахождения сопряженных векторов направлений на движущиеся объекты, который заключается в формировании i-x, j-x пар ортов a(i) и b(j) векторов направлений на объекты в системах координат двух взаимно удаленных на базовое расстояние d0 сканирующих радиометров, вычислении в системе координат первого радиометра смешанного произведения векторов a(i), b(j) и орта τ базового вектора и сохранении тех i-x, j-x неповторяющихся пар ортов, для которых модуль смешанного произведения не превышает малого положительного числа, отличающийся тем, что в последовательности периодов сканирования, начиная со второго, для каждой пары векторов a(i), b(j) вычисляется приращение Δa(i) для орта а(i) умножением длины промежутка времени между двумя моментами времени образования пары ортов a(i) и b(j) на вектор скорости изменения координат орта a(i), определяемый за один период сканирования радиометра, после чего для измененного орта a(i), орта b(i) и орта τ вычисляют их смешанное произведение и, если модуль смешанного произведения не превышает малого положительного числа, то находят в системах координат радиометров оценки дальностей до объекта ra(i), rb(j), векторы пространственных координат объекта Ma(i)=ra(i)a(i), Mb(j)=rb(j)b(j) и вычисляют показатель сопряжения по формуле: 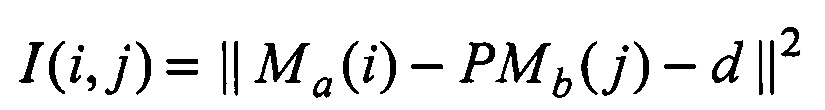 и, если показатель I(i, j) не превышает заданного порога, то вектор Ma(i) и показатель I(i, j) запоминают в отдельных массивах в последовательности периодов сканирования, после чего по истечении заданного числа периодов из указанных массивов извлекают неповторяющиеся группы запомненных векторов пространственных координат объектов с наименьшими суммарными значениями показателей.
и, если показатель I(i, j) не превышает заданного порога, то вектор Ma(i) и показатель I(i, j) запоминают в отдельных массивах в последовательности периодов сканирования, после чего по истечении заданного числа периодов из указанных массивов извлекают неповторяющиеся группы запомненных векторов пространственных координат объектов с наименьшими суммарными значениями показателей.
Алгоритмически способ сводится к следующим операциям.
1. В первом периоде сканирования (n=1, n - номер периода) радиометров формируются орты i-х и j-x направлений an(i), 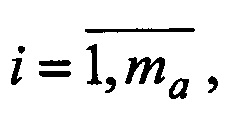 и bn(j),
и bn(j), 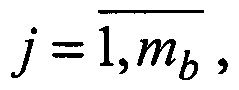 где ma и mb - число ортов в радиометрах.
где ma и mb - число ортов в радиометрах.
1.1. Рассматриваются i-e, j-e варианты соединения ортов в пары. Для каждого i-го, j-го варианта вычисляется показатель J(i, j) необходимого условия сопряжения по формуле (1), который сравнивается с порогом 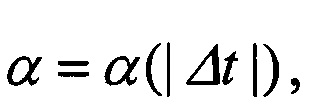 зависящим от модуля разности моментов времени образования ортов Δt=ta(i)-tb(j). Если J(i,j)>α, то данный вариант соединения ортов отвергается.
зависящим от модуля разности моментов времени образования ортов Δt=ta(i)-tb(j). Если J(i,j)>α, то данный вариант соединения ортов отвергается.
1.2. Если J(i,j)≤α, то i-я, j-я пара считается перспективной. Ей присваивается g-й номер группы перспективных векторов, к которой будут присоединяться другие векторы в последующих периодах сканирования (нумерация g - в порядке выполнения неравенства, 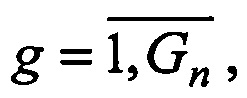 Gn - число групп в n-м периоде). Запоминаются: момент времени T(g)=ta(i) образования орта a(i); начальное значение показателя правдоподобия I(g)=0 g-й группы; орт A(g)=ak(i) или номер орта ia(g)=i.
Gn - число групп в n-м периоде). Запоминаются: момент времени T(g)=ta(i) образования орта a(i); начальное значение показателя правдоподобия I(g)=0 g-й группы; орт A(g)=ak(i) или номер орта ia(g)=i.
2. Во втором и последующих периодах (n=2, 3,…,N) сканирования радиометров также формируются орты i-x и j-x направлений an(i), 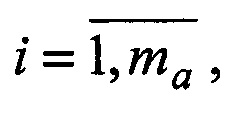 и bn(j),
и bn(j), 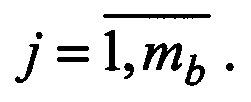
2.1. Рассматриваются i-e, j-e варианты соединения ортов в пары. Каждая i-я, j-я пара ортов an(i) и bn(j) ставятся в соответствие сформированным в предыдущем (n-1)-м периоде g-м группам 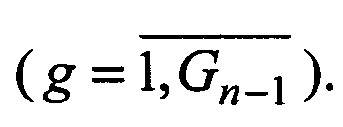 Для орта an(i) вычисляется вектор скорости изменения координат орта за один период сканирования:
Для орта an(i) вычисляется вектор скорости изменения координат орта за один период сканирования:
νn(i)=(1/Δt)⋅[an(i)-A(g)], Δt=ta(i)-Tb(g).
Вычисляется приращение орта Δan(i)=[tb(j)-ta(i)]⋅νn(i) и орт an(i) меняется прибавлением к нему приращения Δan(i).
2.2. Для измененного орта an(i) и орта bn(j) вычисляется показатель J(i, j) необходимого условия сопряжения по формуле (1), который сравнивается с малым положительным числом ε. Если J(i, j)>ε, то данный вариант соединения ортов отвергается.
2.3. Если J(i, j)≤ε, то для an(i) и bn(j) вычисляются оценки дальностей 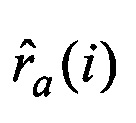 и
и 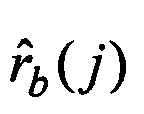 по формуле, полученной на основе минимизации показателя (2) по ra(i) и rb(j). Вычисляются оценки векторов координат предполагаемых объектов:
по формуле, полученной на основе минимизации показателя (2) по ra(i) и rb(j). Вычисляются оценки векторов координат предполагаемых объектов: 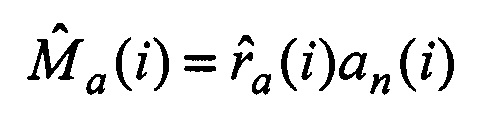 и
и 
2.4. Вычисляется показатель достаточного условия сопряжения I(i, j) по формуле (2), который сравнивается с порогом β. Если I(i, j)>β, то i-я, j-я пара векторов далее не рассматривается.
2.5. Если I(ρ)≤β, то орт an(i) прикрепляется к g-й группе, давая ей продолжение под новым ρ-м номером (нумерация ρ - в порядке выполнения неравенства, 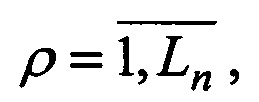 Ln - число групп, сформированных в n-м периоде). Для ρ-й группы запоминаются: момент времени образования орта T(ρ)=ta(i), сам орт А(ρ)=an(i) или номер орта ia(ρ)=i; вектор оценок пространственных координат
Ln - число групп, сформированных в n-м периоде). Для ρ-й группы запоминаются: момент времени образования орта T(ρ)=ta(i), сам орт А(ρ)=an(i) или номер орта ia(ρ)=i; вектор оценок пространственных координат 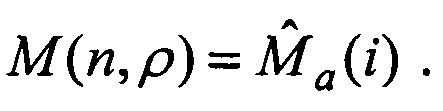 Причем векторы, присоединенные к g-й группе в предыдущих периодах 2, 3,…, n-1, переписываются в массив M(s, ρ),
Причем векторы, присоединенные к g-й группе в предыдущих периодах 2, 3,…, n-1, переписываются в массив M(s, ρ), 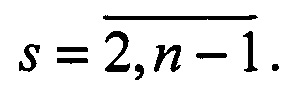 Вычисляется суммарный показатель правдоподобия ρ-й группы: I(ρ)=I(g)+I(i, j).
Вычисляется суммарный показатель правдоподобия ρ-й группы: I(ρ)=I(g)+I(i, j).
2.6. Если g-я группа не получает подтверждения в n-м периоде, то фиксируется пропуск наблюдения и проверяется подтверждение в следующем (n+1)-м периоде. При этом используется определенная логика сброса неподтвержденных групп. Орты an(i) и bn(j), не вошедшие в состав подтвержденных групп, рассматриваются как начальные данные для вновь появляющихся объектов. Для них выполняются операции п. 1 и осуществляется анализ на подтверждение в последующих периодах сканирования.
2.7. По окончании операций в n-м периоде, где 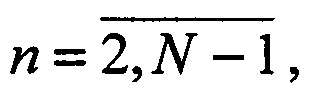 меняются обозначения: номер группы ρ меняется на g, число групп Ln - на Gn.
меняются обозначения: номер группы ρ меняется на g, число групп Ln - на Gn.
3. После выполнения операций п. 2 в последнем N-м периоде среди LN ρ-х групп 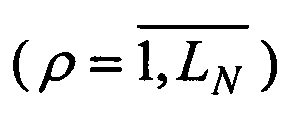 выделяются
выделяются 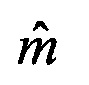 групп, которые характеризуются наименьшими значениями показателей I(ρi),
групп, которые характеризуются наименьшими значениями показателей I(ρi), 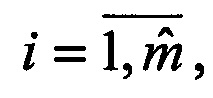 и не имеют общих векторов в массиве М(n, ρ),
и не имеют общих векторов в массиве М(n, ρ), 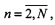
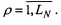 Вначале выделяется номер ρ1 группы с наименьшим показателем I(ρ1), этот номер исключается из дальнейшего рассмотрения в массивах I(ρ) и М(n, ρ). Затем выделяется номер ρ2 и т.д. Допускается возможность выделения групп с минимальным количеством π общих векторов (например, π=1 или 2).
Вначале выделяется номер ρ1 группы с наименьшим показателем I(ρ1), этот номер исключается из дальнейшего рассмотрения в массивах I(ρ) и М(n, ρ). Затем выделяется номер ρ2 и т.д. Допускается возможность выделения групп с минимальным количеством π общих векторов (например, π=1 или 2).
4. Для 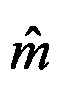 выделенных групп у оценки векторов пространственных координат объектов M(n, ρi),
выделенных групп у оценки векторов пространственных координат объектов M(n, ρi), 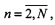
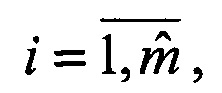 передаются на алгоритм определения траекторных параметров движения
передаются на алгоритм определения траекторных параметров движения 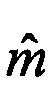 обнаруженных объектов и их сопровождения (
обнаруженных объектов и их сопровождения (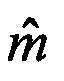 - оценка числа m).
- оценка числа m).
Предложенный способ позволяет находить сопряженные пары ортов векторов направлений на объекты в системе двух радиометров в условиях движущихся объектов и случайных помех. Это дает возможность повысить вероятность обнаружения всех движущихся объектов и точность определения их пространственных координат по сравнению с методами, не учитывающими движение объектов. Способ может найти применение в существующих радиотехнических и оптических системах пассивного видения при наблюдении за несколькими объектами.
Литература
1. Пассивная радиолокация: методы обнаружения объектов / Под ред. Р.П. Быстрова и А.В. Соколова. М.: Радиотехника, 2008. 320 с.
2. Цифровая обработка изображений в информационных системах: учеб. пособие / И.С. Грузман, B.C. Киричук и др. Новосибирск: Изд-во НГТУ, 2002. 352 с.
Способ нахождения сопряженных векторов направлений на движущиеся объекты, заключающийся в формировании i-x, j-x пар ортов (i) и b(j) векторов направлений на объекты в системах координат двух взаимно удаленных на базовое расстояние d сканирующих радиометров, вычислении в системе координат первого радиометра смешанного произведения векторов (i), b(j) и орта τ базового вектора d=dτ и сохранении тех i-x, j-x неповторяющихся пар ортов, для которых модуль смешанного произведения не превышает малого положительного числа, отличающийся тем, что в последовательности периодов сканирования начиная со второго для каждой пары векторов (i), b(j) вычисляется приращение Δ(i) для орта (i) умножением длины промежутка времени между двумя моментами времени образования пары ортов (i) и b(j) на вектор скорости изменения координат орта (i), определяемый за один период сканирования радиометра, после чего для измененного орта (i), орта b(i) и орта τ вычисляют их смешанное произведение и, если модуль смешанного произведения не превышает малого положительного числа, то находят в системах координат радиометров оценки дальностей до объекта r(i), r(j), векторы пространственных координат объекта M(i)=r(i)(i), M(j)=r(j)b(j) и вычисляют показатель сопряжения по формуле:I(i, j)=||M(i)-PM(j)-d||, где Р - матрица поворота осей координат, и, если показатель I(i, j) не превышает заданного порога, то вектор M(i) и показатель I(i, j) запоминают в отдельных массивах в последовательности периодов сканирования, после чего по истечении заданного числа периодов из указанных массивов извлекают неповторяющиеся группы запомненных векторов пространственных координат объектов с наименьшими суммарными значениями показателей.
