Способ защиты информации в облачных вычислениях с использованием гомоморфного шифрования

Перекрестная ссылка на родственную заявку

Данная заявка является обыкновенной заявкой на патент по отношению к предварительной заявке США №61556507, поданной 7 ноября 2011 г., содержание которой включено в состав данной заявки для справки.

Область техники, к которой относится изобретение

Изобретение в общем относится к способам шифрования информации. Более точно, изобретение относится к способам защиты информации в системах облачных вычислений с использованием гомоморфного шифрования.

Уровень техники

В информатике облако - вычислительный ресурс, который предоставляется пользователю поставщиком услуг. Все облачные услуги и инфраструктура реализуются поставщиком услуг, причем технические детали реализации скрыты от пользователя. Выделяются три модели обслуживания (три класса).

Инфраструктура как услуга. Поставщик услуги обеспечивает функциональность виртуальных вычислительных машин и контролирует их инфраструктуру, которая может создаваться, изменяться или удаляться клиентом (пользователем). Пользователь может самостоятельно решать, как ему использовать предоставляемую услугу. Примером подобной системы является "Amazon Web Services" - инфраструктура платформы веб-услуг в облаке, реализованная компанией Amazon.

Платформа как услуга. Поставщик предоставляет пользователю вычислительную платформу для запуска и выполнения программ-приложений. Поставщик услуги обеспечивает функциональность вычислительной платформы, а пользователь только предоставляет программу-приложение для запуска на предоставленной ему вычислительной платформе. Облачная инфраструктура может использоваться таким образом для решения специализированных задач или классов задач. Примером подобной системы является "Google Арр Engine" - инфраструктура и сервис хостинга сайтов и web-приложений, реализованная компанией Google.

Программное обеспечение как услуга. Поставщик предоставляет пользователю для решения определенных задач полностью функциональное прикладное программное обеспечение, работающее в облачной инфраструктуре. Поставщик услуги отвечает и за саму облачную вычислительную инфраструктуру, на которой выполняется приложение, и за разработку требуемого для предоставления услуги прикладного программного обеспечения. Подобная облачная вычислительная структура имеет специфическую, узкую область применения. Примером подобной системы является услуга электронной почты "Gmail", реализованная компанией Google.

Только первые два из перечисленных классов позволяют выполнять в облаке приложения пользователя. Защищенное облачное вычисление - система, в которой операции, выполняемые в облаке, не могут быть распознаны извне. Кроме того, требуется, чтобы часть информации хранилась в облаке в течение длительного времени в защищенном от постороннего доступа виде. И, кроме того, требуется, чтобы передача информации в облако была защищена от постороннего доступа.

Таким образом, признаками защищенного облачного вычисления являются:

- защищенное от постороннего доступа хранение информации в облаке;

- защищенная от постороннего доступа обработка информации в облаке;

- защищенная от постороннего доступа передача информации в облако и из облака.

Обработка информации в облаке выполняется непрерывно. Проходящая через облако информация нередко содержит важные персональные данные, доступ к которым с учетом технических ограничений облака все же возможен. Единственным способом защиты информации является шифрование файлов, так, чтобы злоумышленники не смогли прочесть содержащуюся в них информацию.

Таким образом, желательно иметь систему для защищенных облачных вычислений. Такая система должна оперировать информацией в зашифрованном виде, которая не может быть прочтена даже в том случае, если к файлу появился доступ для посторонних. Информация должна передаваться в облако уже в зашифрованном виде. Шифрование должно выполняться на стороне пользователя, так, чтобы даже сервис облачных вычислений не знал, каким образом информация зашифрована.

Кроме того, облако должно быть способно обрабатывать зашифрованную информацию без ее расшифровки. В противном случае облако будет всего лишь хранилищем зашифрованной информации, и выполнение любой операции потребовало бы отправки данных обратно пользователю для расшифровки и, затем, снова отправки данных в облако для обработки. Существует альтернативный способ - отправка в облако ключа шифрования для расшифровки данных. Однако такой способ подвергает опасности перехвата информацию, находящуюся в облаке.

Обычные облачные услуги не обеспечивают в полной мере безопасное хранение информации. В некоторых редких случаях информация может быть зашифрована на стороне пользователя. В других вариантах реализации информация шифруется с использованием ключа, который хранится в том же самом облаке. Оба варианта ненадежны и неудобны для эффективного выполнения облачных вычислений. Пусть, например, налоги физических лиц и предприятий вычисляются сторонними службами третьих лиц. Очевидно, желательно не раскрывать некоторую информацию о доходах третьим лицам. Личные данные должны быть зашифрованы и отправлены на обработку. Затем результаты передаются обратно и расшифровываются принимающей стороной.

Таким образом, существует потребность в технологии обработки данных в облаке в зашифрованном виде без расшифровки. Соответственно, требуется способ гомоморфного шифрования данных для облачных вычислений, чтобы информация могла обрабатываться без расшифровки.

Раскрытие изобретения

Настоящее изобретение относится к системам и способам защиты информации в системе облачных вычислений путем гомоморфного шифрования, что в существенной мере устраняет один или более недостатков подобных технологий.

Способ защиты облачного вычисления включает гомоморфное шифрование данных. Полностью гомоморфное шифрование дает возможность обрабатывать информацию в облаке без ее дешифровки.

Гомоморфное шифрование является разновидностью шифрования, при котором для операций над незашифрованными данными имеются соответствующие аналоги-операции над зашифрованными данными. Если операция О применяется к зашифрованным данным, а данные затем расшифровываются, то результат оказывается тем же, что и при выполнении операции-аналога О над незашифрованными данными.

В варианте осуществления предлагается специальная схема гомоморфного шифрования. Предлагаемая схема может использоваться как в алгебраическом, так и в аналитическом подходе. Услуга облачных вычислений реализуется на сервере. Клиент шифрует данные и отправляет их на сервер. Этот сервер выполняет вычисления, не прибегая к дешифровке информации, и возвращает клиенту результат вычислений в зашифрованном виде. Клиент расшифровывает результат, причем этот результат совпадает с результатом такого же вычисления, если бы оно было выполнено над незашифрованными данными.

Дополнительные особенности и преимущества настоящего изобретения будут разъяснены в следующем далее описании осуществления изобретения. Частично они станут понятны из описания, либо они будут выявлены практикой использования изобретения. Достоинства изобретения будут реализованы и получены в структуре, частично раскрытой в прилагаемом описании и формуле изобретения, а также в прилагаемых чертежах.

Следует учитывать, что и предшествующее общее описание, и последующее детальное описание приводятся в качестве примера и в целях разъяснения и предназначены для лучшего объяснения сущности заявленного изобретения.

Краткое описание чертежей

Прилагаемый чертеж, включенный в состав заявки для дальнейшего разъяснения сущности изобретения и являющийся составной частью настоящего описания, иллюстрирует варианты осуществления изобретения и служит совместно с описанием для объяснения основ настоящего изобретения. На чертеже показано:

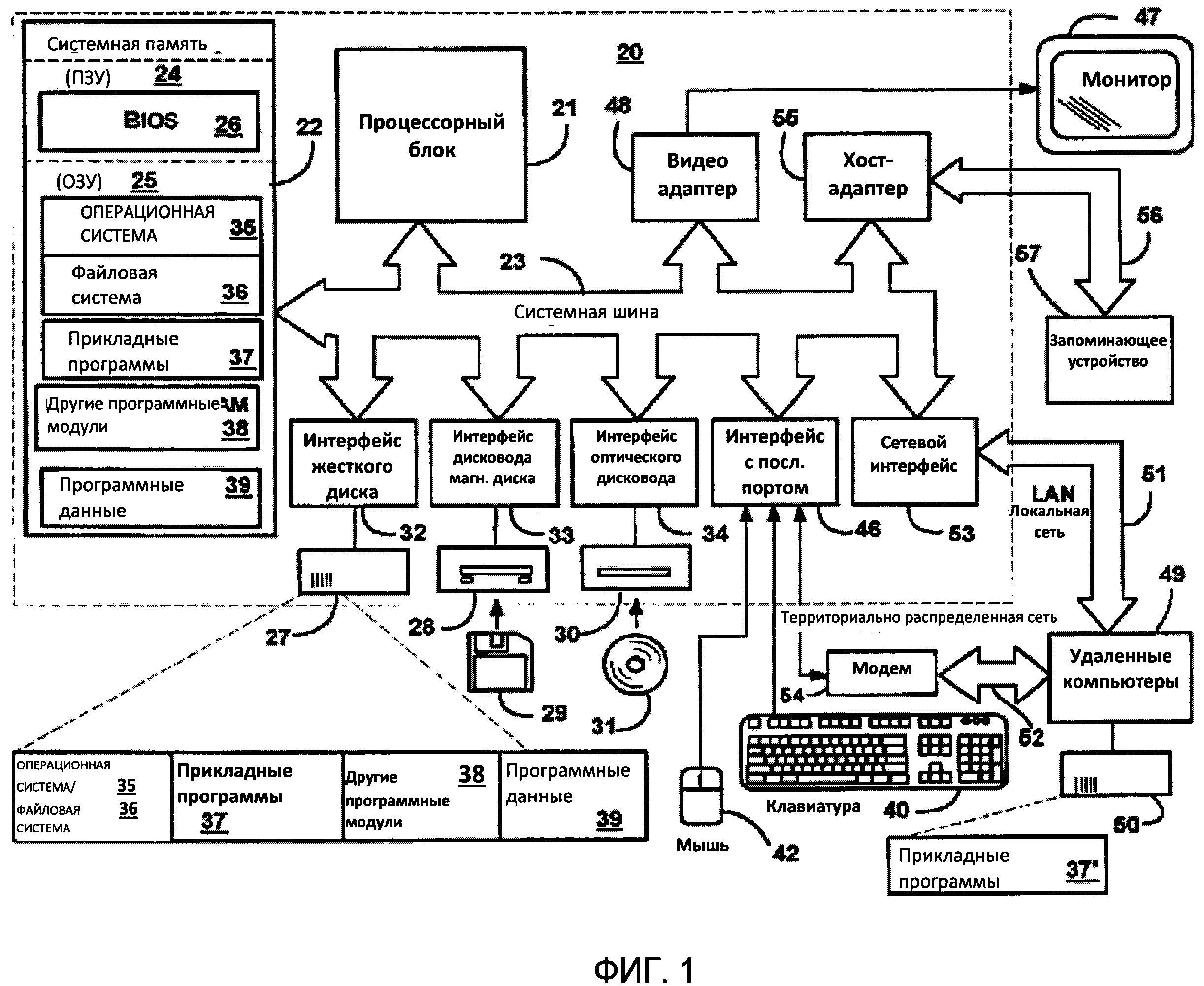
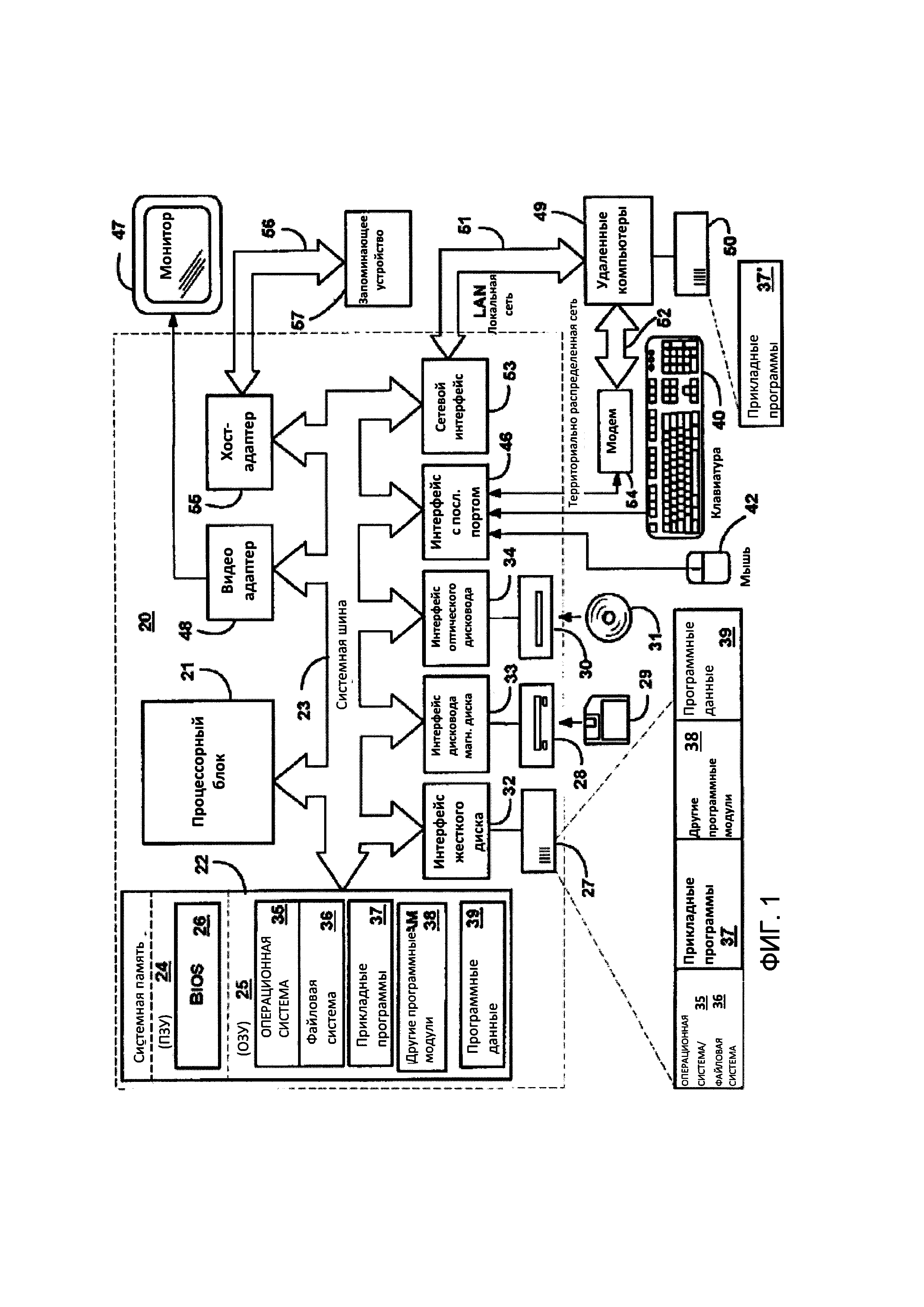
на фиг. 1 - структурная схема варианта компьютерной системы, которая может использоваться совместно с настоящим изобретением.

Осуществление изобретения

Далее приводится подробное описание вариантов осуществления настоящего изобретения.

Представлен способ гомоморфного шифрования информации для облачных вычислений. Полностью гомоморфное шифрование позволяет обрабатывать данные внутри облака без их дешифровки. Схемы полностью гомоморфного шифрования являются гибкими. Криптосистема (в данном случае - набор математических операций) является гибкой, если возможно преобразовать данные из одной зашифрованной формы в другую без промежуточной дешифровки.

Принцип гомоморфизма может быть описан следующим образом. Пусть имеется преобразование ƒ, переводящее А в В, то есть ƒ: А→В, где А и В - кольца (алгебраические множества), для которых определены операции сложения и умножения, а также, возможно, нулевая и единичная операция. Тогда ƒ является гомоморфным преобразованием (гомоморфизмом) колец, если

ƒ(a_+Ab)=ƒ(a)_+Bƒ(b),

ƒ(a×_Ab)=ƒ(a)×_Bƒ(b),

ƒ(1_A)=1_B,

ƒ(0_A)=0_B.

Гомоморфные операции по определению защищены от постороннего доступа к информации, что является неотъемлемым свойством любого гомоморфного шифрования. Гомоморфное шифрование является разновидностью шифрования, при котором операции над незашифрованными данными имеют соответствующие им операции-аналоги над зашифрованными данными. Если операция О выполняется над зашифрованными данными, а затем результат дешифровать, то он оказывается тем же, как если бы операция О выполнялась над незашифрованными данными.

Для полностью гомоморфного шифрования указанное условие справедливо для всех операций. В противном случае шифрование является частично гомоморфным. Полностью гомоморфное шифрование удовлетворяет всем требованиям защиты информации для защищенных облачных сервисов. Иными словами, полностью гомоморфное шифрование позволяет шифровать данные и выполнять операции над зашифрованными данными без дешифровки.

В варианте осуществления представлена специальная схема гомоморфного шифрования. Предлагаемая схема может использоваться как в алгебраическом, так и в аналитическом подходе.

Алгебраический подход может быть описан следующим образом. Формальные полиномы образуют кольцо А[x] относительно операций сложения и умножения.

Пример гомоморфизма колец:

1. Преобразование ƒ(x)=x+c, ƒ^*: А[x]→А[x].

Результирующая (преобразованная) операция ƒ^*, сформированная из операции ƒ, должна быть гомоморфизмом колец.

В случае формальных полиномов (рассматриваются полиномы одинаковой степени)

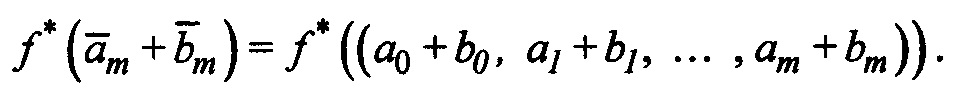
Соответствующий результирующий полином

R(x)=(a₀+b₀)+(a₁+b₁)x+…+(a_m+b_m)x^m,

причем ƒ(R(x))=(a₀+b₀)+(a₁+b₁)(x+c)+…+(a_m+b_m)(x+c)^m.

С другой стороны, если Р(x) и Q(x) соответствуют формальным полиномам 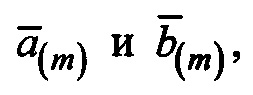то

ƒ(P(x))+ƒ(Q(x))=

=а₀+а₁(x+с)+…+a_m(x+с)^m+b₀+b₁(x+c)+…+b_m(x+c)^m.

Соответственно,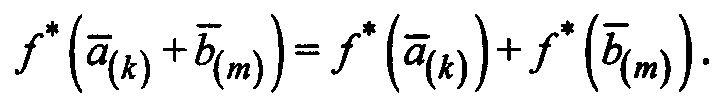

Произведение может быть описано аналогичным образом:

Р(x)⋅Q(x)=a₀b₀+(a₀b₁+a₁b₀)x+(a₀b₂+a₁b₁+a₂b₀)x²+…+a_mb_mx^m+m,

ƒ^*(P(x)⋅Q(x))=a₀b₀+(a₀b₁+a₁b₀)(x+c)+(a₀b₂+a₁b₁+a₂b₀)(x+c)²+…

+…+a_mb_m(x+c)^m+m.

Тогда

ƒ^*(P(x))⋅ƒ^*(Q(x))=a₀b₀+(a₀b₁+a₁b₀)(x+с)+(a₀b₂+a₁b₁+a₂b₀)(x+c)²+…

+…+a_mb_m(x+c)^m+m.

Последнее выражение совпадает с ƒ^*(Р(x)⋅Q(x)).

Соответственно,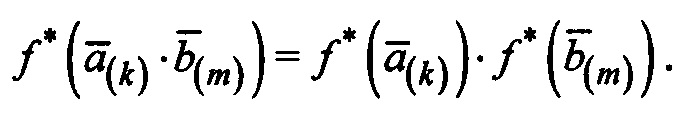

Следует также обратить внимание, что ƒ преобразует 0 в 0, а также 1 в 1.

В результате, согласно определению, преобразование ƒ создает гомоморфизм колец ƒ^* из ƒ. Иными словами,

ƒ^*(a+A[x]b)=ƒ^*(a)+A[x]ƒ^*(b).

Рассмотрим преобразование g(x)=c⋅x.

Необходимо показать, что g*, преобразованное из g, также является гомоморфизмом колец.

Рассмотрим сумму

g^*(R(x))=a₀+b₀+(a₁+b₁)cx+…+(a_m+b_m)(сх)^m..

g^*(P(x))+g(Q(x))=a₀+a₁(cx)+…+a_m(сх)^m+b₀+b₁(сх)+…+b_m(cx)^m.

Соответственно,

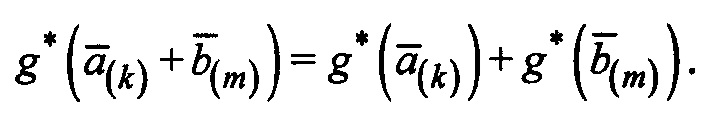
Рассмотрим произведение

g^*(Р(x)⋅Q(x))=a₀b₀+(a₀b₁+a₁b₀)(cx)+

+(a₀b₂+a₁b₁+a₂b₀)(cx)²+…+a_mb_m(cx)^m+m.

Тогда

g^*(P(x))⋅g(Q(x))=

=a₀b₀+(a₀b₁+a₁b₀)(cx)+(a₀b₂+a₁b₁+a₂b₀)(cx)²+…+a_mb_m(cx)^m+m.

Последнее выражение соответствует g^*(P(x)⋅Q(x)).

Соответственно,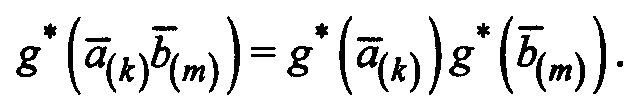

Таким образом, преобразование g преобразует 0 в 0, а также 1 в 1.

Поэтому преобразование g формирует гомоморфизм колец g*:

g^*(a+A[x]b)=g^*(a)+A[x]g*(b).

Любой полином Р(x)=а₀+a₁x+а₂х²+…+a_mx^m формирует гомоморфизм Р* колец формального полинома. Поэтому:

Р^*: А[x] → А[x]

1. P^*(a+A[x]b)=P^*(a)+A[x]P^*(b).

2. P^*(a⋅A[x]b)=P^*(a)⋅A[x]P^*(b).

3. Р^*(0_A[x])=0_A[x].

4. Р^*(1_A[x])=1_A[x].

Гомоморфное шифрование на множестве Z₂[x].

Пусть кольцо состоит только из двух элементов, 0 и 1.

Требуется зашифровать два элемента с использованием описанного выше алгоритма для последующего выполнения операций над ними. Элемент z₁ имеет формальный полином (z₁, a₁, a₂, …, a_m). Применение гомоморфизма Р дает формальный полином (q₀, q₁, q₂, …, q_m+р).

Шифрование z₂ приводит к (r₀, r₁, r₂, …, r_m+p).

Соответственно, после того, как операции выполнены, формируется формальный полином. Этот полином после расшифровки дает результат в первой позиции. Если над полиномами выполняются операции (оба полинома являются результатами шифрования z₁ и z₂) вида z₁+ƒ₁(z₁)+ƒ₂(z₁) и z₂+g₁(z₂)+g₂(z₂), то умножение и сложение приведут к результату вида

(z₁*z₂+z₁)+(ƒ₁(z₁)*g₁(z₂)+ƒ₁(z₁))+….

Первый элемент в скобках может использоваться как результат операции, если из данных удаляется "хвост", который несущественен для решаемой задачи. Данный пример показывает, что в предложенном способе функциональность достигается за счет выполнения вычислений более сложным образом и путем увеличения необходимого числа вычислений, причем даже для простых арифметических операций. Умножение и сложение могут рассматриваться как операции над матрицами. Размер матрицы выясняется во время расшифровки, это необходимо для идентификации значимой информационной части элемента.

Например, в случае выполнения операции 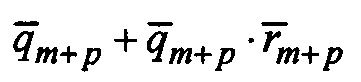после расшифровки первая позиция в результирующем формальном полиноме будет содержать z₁+z₁⋅z₂.

Например, для нахождения значения m₁+m₂ сравниваются элементы полиномов (m₁, а, b) и (m₂, с, d). Применяется гомоморфизм, образованный полиномом Р(x)=p+q⋅x. Получающиеся в результате полиномы имеют вид

(m₁+ар+bp², aq+2bpq, bq²),

(m₂+cp+dp², cq+2dpq, dq²).

Их суммирование дает

R=(m₁+m₂+ap+cp+bp²+dp², aq+cq+2bpq+2dpq, bq²+dq²).

Для расшифровки полином

R(x)=m₁+m₂+ap+cp+bp²+dp²+(aq+cq+2bpq+2dpq)x+[bq²+dq²)x²

делится на p+qx, что дает остаток m₁+m₂, представляющий собой результат.

При умножении скобки не раскрываются, и формальный полином имеет вид:

m₁+a(p+qx)+b(p+xq)²,

m₂+c(p+qx)+d(p+xq)².

Результат перемножения зашифрованных полиномов:

m₁m₂+(m₁c+m₂a)(р+qx)+(m₁d+ас+m₂b)(р+qx)²+

+(ad+bc)(p+qx)³+bd(p+qx)⁴.

Следует обратить внимание, что если раскрыть скобки, то станет невозможно что-либо восстановить без знания р+qx.

Однако если результирующий полином делится на р+qx, то получается требуемый элемент.

Аналитический подход может быть описан следующим образом. Рассмотри класс функций на множестве M со значениями, расположенными на кольце A. Такие функции образуют кольцо F=А(М) относительно операций дискретного сложения и умножения. Пусть G=A(S), где S - математическое множество. Рассмотрим преобразование φ: М→S. Такое преобразование может быть названо подстановкой переменных x=φ(у), x ∈ S, y ∈ М. Такая подстановка переменных создает гомоморфизм φ^* колец функций: φ^*: F→G.

Это утверждение может быть доказано следующим образом. Пусть ƒ(x) и g(x) - функции кольца F, а φ^*(ƒ(x)) и φ^*(g(x)) - функции кольца G.

1. ƒ(x)+g(x)→φ^*(ƒ(x)+g(x))=ƒ(φ(x))+g(φ(x))=φ^*(ƒ(x))+φ^*(g(_X)).

2. ƒ(x)⋅g(x)→φ^*(ƒ(x)⋅g(x))=ƒ(φ(x))⋅g(φ(x))=^*(ƒ(x))⋅φ^*(g(x)).

3. 1_F→1_G.

4. 0_F→0_G.

Таким образом, φ^* действительно является гомоморфизмом колец функций.

Один пример может использовать полиномы колец действительных чисел, целых чисел или простых чисел.

R[x] - кольцо полиномов.

Любой полином Р(x) создает гомоморфизм Р^*: R[x]→R[x].

Возможна следующая реализация в модели взаимодействия клиент-сервер. Клиенту требуется выполнить вычисления на сервере таким образом, чтобы сервер не знал, что за данные используются в вычислениях. Например, клиенту требуется вычислить значение функции-полинома ƒ(x₁, x₂, …, x_n) в точке (а₁, a₂, …, a_n). Для этого выполняются следующие шаги.

- на стороне клиента случайным образом выбирается секретный ключ x₀, причем x₀ - действительное число;

- для каждого числа a_i - элемента вектора значений выбираются b_i и c_i таким образом, что b_ix₀+c_i=a_i;

- линейные полиномы в виде b_ix+c_i совместно с функцией-полиномом ƒ(x₁, …, x_n) передаются на сервер;

- клиент запрашивает сервер подставить вместо x_i линейные полиномы. Сервер подставляет полиномы в функцию ƒ:

ƒ(b₁x+c₁, …, b_nx+c_n).

Затем сервер раскрывает скобки и передает результат клиенту. Таким образом, клиент получает коэффициенты полинома, несущие требуемую информацию о значении в точке х₀.

Клиент подставляет х₀ в результирующую функцию-полином и находит требуемое значение. Следует обратить внимание, что сервер не знает значение аргумента, для которого клиенту требуется вычислить значение функции.

Такая схема гомоморфного шифрования позволяет защитить операции и позволяет сортировать зашифрованные данные. Поскольку операции выполняются над действительными числами, то точка х₀ обладает окрестностью, в которой линии, соответствующие a_ix+b_i, не пересекаются. В точке x₀ сохраняется корректный порядок, однако он сохраняется неизменным в окрестности.

Использование действительных чисел позволяет получить преимущество ортогональности преобразований, иными словами, различные исходные данные будут всегда приводить к различным зашифрованным результатам. Кроме того, для любой пары зашифрованных текстовых строк возможно идентифицировать точку x₀ так, что в ее окрестности линейные функции, полученные из дешифрованных результатов, сохраняют свои относительные значения (меньше-больше), как до, так и после шифрования и дешифровки. Для каждой пары существует характерная точка хо, которая может быть идентифицирована без расшифровки. Использование таких точек x₀ позволяет сортировать список, причем список не содержит одинаковых элементов.

Соответственно, элемент может быть передан серверу без раскрытия секретного ключа.

В варианте осуществления используются следующие криптосхемы полностью гомоморфного шифрования.

Криптосхема Доминго-Феррэ (от английского - Domingo-Ferre).

Выбираются два простых числа р и q, их произведение n=pq. Также выбирается положительное целое число d. Открытым ключом является (d, n). Затем используются элементы r_p и r_q из Z_p и Z_q, которые образуют перемножаемые подгруппы соответственно в Z_p и Z_q. Секретным ключом является (p, q, r_p, r_q).

Шифрование выполняется следующим образом.

Для того, чтобы зашифровать элемент a ∈ Z_n, его следует представить в виде суммы

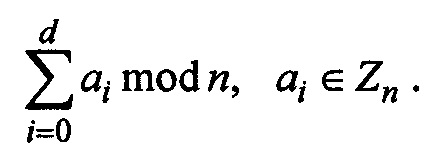
В результате зашифрованное сообщение будет иметь вид:

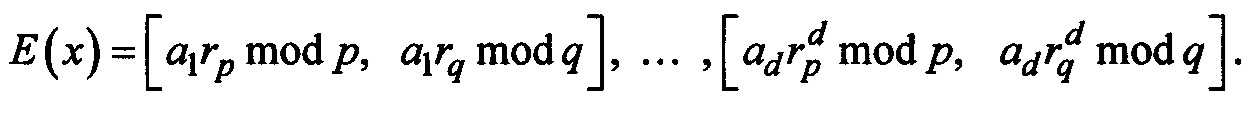
Расшифровка выполняется с использованием китайской теоремы об остатках.

Альтернативный вариант реализации криптосхемы заключается в следующем. Чтобы зашифровать элемент a ∈ Z_n, выбирается полином ƒ(x) с коэффициентами из Z_n, ƒ(x)=а₀+a₁x+,…,+a_dx^d, причем ƒ(1)=а.

Иными словами, а=а₀+а₁+,…,+a_n является аналогом суммы 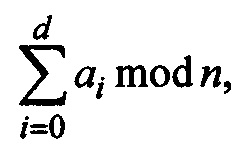a_i ∈ Z_n. Пусть r_p и r_q будут теми же, что и в типовой реализации схемы, описанной выше.

Тогда шифрование состоит в применении гомоморфизмов φ_p=r_py и φ_q=r_qy к полиному ƒ(x). Зашифрованное сообщение образуется из пары коэффициентов полиномов ƒ_p(y)=ƒ(φ_p(x)) и ƒ_q(y)=ƒ(φ_q(x)) по модулю p и q соответственно.

В соответствии с вариантом осуществления может использоваться другая криптосхема Крейга-Джентри (от английского - Craig-Gentry). Шифрование по этой схеме полностью гомоморфное и основано на использовании идеальных решеток. Вычисления выполняются над полем Z₂. Два элемента могут рассматриваться как биты. Пусть m - некоторый бит, имеющий соответствующий номер, выбираемый по следующему правилу. Выбираются три числа r, k, q, причем r<<k. Секретным ключом считается k.

Вычисляется c=2r+m+(2k+1)q. Следует учесть, что

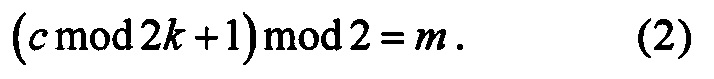
Это означает, что значение с не определяет бит m (1), однако если известен k, то бит m может быть восстановлен однозначно по (2).

Операции над битами по рассматриваемой криптосхеме будут иметь следующий вид.

Пусть m₁ и m₂ являются битами. Тогда

c₁=2r₁+m₁+(2k+1)q₁,

c₂=2r₂+m₂+(2k+1)q₂,

с₁+с₂=2r₁+m₁+(2k+1)q₁+2r₂+m₂+(2k+1)q₂=

=2(r₁+r₂)+m₁+m₂+(2k+1)(q₁+q₂).

Если 2(r₁+r₂)+m₁+m₂<(2k+1), то

((c₁+c₂)mod(2k+1))mod2=(m₁+m₂)mod2.

Произведение вычисляется аналогично:

c₁c₂=(2r₁+m₁+(2k+1)q₁)(2r₂+m₂+(2k+1)q₂)=

=2(2r₁r₂+r₁m₂+r₂m₁)+m₁m₂+(2k+1)q,

где

q=2r₁q₂+m₁q₂+2r₂q₁+m₂q₁+q₁q₂(2k+1).

Изложенный подход может быть реализован следующим образом.

Пусть m₁ и m₂ - два бита, участвующие в операции, выполняемой в облаке. После процедуры шифрования невозможно определить значения этих битов. Возможны следующие пары значений: (0,0), (0,1), (1,0) и (1,1). Записанные упорядоченным образом, эти пары имеют вид:

Нижняя строка - это номер одного из четырех возможных состояний. Приведенная таблица содержит все возможные состояния битов пары. Пусть требуется вычислить функцию ƒ(m₁, m₂) двух аргументов. Функция ƒ с учетом всех возможных значений m₁ и m₂ принимает одно из четырех различных значений. Взлом шифра состоит в угадывании номера столбца в таблице. Иными словами, номер столбца в таблице является секретным ключом.

Согласно другом варианту осуществления, рассматриваются классы полиномиальный функций, например, множество полиномов двух переменных на поле Z₂. Все эти функции имеют вид а₀1+a₁x+а₂у+а₃ху. Множество функций образует кольцо, в котором степень не возрастает после перемножения, поскольку справедливо:

х²=х, у²=у.

В данном случае гомоморфизмы образуются только за счет аффинного преобразования.

Пусть m₁, m₂ являются парами битов, обладающими соответствующими полиномами

m₁+a₁x+а₂у+а₃ху,

m₂+b₁x+b₂y+b₃xy.

Гомоморфизм за счет афинного преобразования имеет вид:

x=u+ν,

y=ν+1.

Тогда полиномы преобразуются в другие новые полиномы:

m₁+a₁(u+ν)+a₂(ν+1)+a₃(u+ν)(ν+1)=m₁+a₂+(a₁+a₃)u+(a₂+a₃)ν+a₃νν=

=m₁+a₂+(a₁+a₃)u+(a₂+a₃)ν+a₃ν=m₁+а₂+(a₁+a₃)u+a₂ν,

для второго бита по аналогии получаем:

m₂+b₂+(b₁+b₃)u+b₂ν.

Затем указанные полиномы передаются на обработку в облаке.

Если требуется вычислить произведение m₁m₂, то выполняются следующие вычисления:

[m₁+a₂+(a₁+а₃)u+a₂ν][m₂+b₂+(b₁+b₃)u+b₂ν]=(m₁+a₂)(m₂+b₂)+…

Клиенту возвращается полином той же степени. Клиент выполняет обратное преобразование:

u=x+у+1,

ν=y+1,

и использует коэффициент свободного члена, который равен m₁m₂.

В соответствии с другим вариантом осуществления, степени не изменяются, полем является Z_p, где p - простое число.

Кольцом является Z_p[x]/R(x), где R(x) - полином степени d с обратным коэффициентом (при большей степени). Тогда Z_p[x]/R(x) - кольцо полиномов степени d-1. Кольца типа Z_p[x]/R(x) создаются в кодах с коррекцией ошибок. Засекреченные вычисления для элементов кольца Z_p[x]/R(x) дают полиномы той же степени (степень не возрастает).

Если требуется перемножить два полинома ƒ(x), g(x) ∈ Z_p[x]/R(x), то выбирается секретный полином x=u(y) и формируются полиномы ƒ(u(y)), g(u(y)) и R(u(y)). Все три полинома передаются на сервер, где вычисляется произведение ƒ(u(y))×g(u(y)) в кольце Z_p[y]/R(u(y)).

Возвращаемый клиенту результат восстанавливается по процедуре, описанной выше.

Изложенные выше варианты осуществления могут использоваться совместно с коэффициентами любого конечного поля. Иными словами, Z_p может быть любым конечным полем.

Согласно другому варианту осуществления, умножение может выполняться на полях Галуа.

Пусть, например, требуется секретным образом выполнить операцию на поле G(2⁷)=G(128).

Пусть m₁, m₂ ∈ G(2⁷).

Множество полиномов двух переменных имеет вид

G(2⁷)[x,y]/(x²-x, у²-у).

Эти полиномы имеют вид а₀1+a₁x+а₂у+а₃ху, где а₀, а₁, а₂, a₃ ∈ G(2⁷).

Тогда умножение имеет вид:

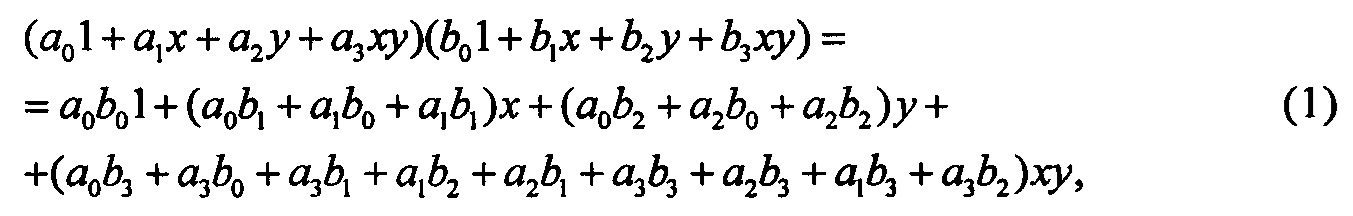
где a_ib_j - произведение из G(2⁷).

Рассчитывается пара соответствующих полиномов

m₁+a₁x+а₂у+а₃ху,

m₂+b₁x+b₂y+b₃xy

для пары элементов m₁, m₂ ∈ G(2⁷).

Затем выполняется замена переменных

x=u+ν,

y=ν+1.

В результате

m₁+а₂+(а₁+а₃)u+a₂ν,

m₂+b₂+(b₁+b₃)u+b₂ν.

Затем данные могут быть отправлены на сервер для выполнения вычислений (например, для вычисления произведения m₁m₂) согласно правилам умножения на поле G(2⁷).

Результат возвращается клиенту, выполняется обратная замена переменных. Альтернативный вариант состоит в выборе в качестве секретного ключа точки с координатами (х₀,у₀).

Коэффициенты полинома выбираются по правилу:

b₀1+b₁x+b₂y+b₃xy,

а ₀1+a₁x+а₂у+a₃xy.

Тогда

m₁=а₀1+а₁х₀+а₂у₀+a₃x₀y₀,

m₂=b₀1+b₁x₀+b₂y₀+b₃x₀y₀.

Полученные полиномы передаются на сервер для выполнения вычислений. Когда результат возвращается клиенту, для расшифровки вычисленного значения в полином подставляются координаты секретной точки (то есть секретный ключ). Следует обратить внимание, что для предыдущего вычисления координаты секретной точки были (0, 1).

В другом варианте осуществления коэффициенты берутся из G(2⁷). Тогда решение - чисто алгебраическое, поскольку значение в секретной точке не существенно.

Следует обратить внимание, что для всех операций на полях Галуа и с полиномами могут использоваться различные способы. Один из примеров описан авторами Шей Гуэрон и Майкл Е. Кунавис в публикации "Команда умножения без переноса компании Интел и ее использование для вычислений в режиме Галуа/сумматор" (от английского Shay Gueron, Michael Е. Kounavis, "Intel® Carry-Less Multiplication Instruction and its Usage for Computing the GCM Mode"), приводимой здесь в качестве ссылки.

Согласно варианту осуществления, гомоморфное шифрование используется для выполнения засекреченных облачных вычислений. Математические модели были описаны выше. Соответствующее программное обеспечение (приложение) может быть реализовано на языке программирования Java, однако выбор конкретного языка программирования не ограничивает настоящее изобретение. Приложение использует собственную (проприетарную) библиотеку, которая выполняет вычисления (например, сложение, вычитание, умножение, деление, вычисление квадратного корня, вычисление корня n-й степени, вычисление экспоненциальной функции и т.д.) над полиномами и рациональными функциями. Согласно варианту осуществления, указанная библиотека предназначена для выполнения конфиденциальных (т.е. секретных) вычислений.

Согласно варианту осуществления, работа клиента организована следующим образом. Приложением на стороне клиента является аплет программы-браузера, который имеет поле ввода и управляющие кнопки, соответствующие числам и операциям. Клиент вводит в поле ввода математическое выражение, содержание действительные числа, скобки, символы операций и функций. Выражение из поля ввода преобразуется в функцию ƒ(x₁, x₂, …, x_n) в точке (а₁, а₂, …, a_n), где а₁, а₂, …, a_n - реальные числа из состава выражения.

Затем выполняется синтаксический анализ выражения, введенного клиентом в поле ввода. Для каждого реального числа назначается уникальная переменная (a₁, а₂, …, a_n). Функция представляется в форме строки. При нажатием пользователем кнопки "равенство" ("=") реальные числа (а₁, а₂, …, a_n) кодируются набором полиномов. Затем на сервер отправляется запрос, содержащий закодированные числа и значения функций для этих чисел.

Полиномы для реальных чисел формируются следующим образом:

- секретным ключом является выбранное случайным образом число х₀;

- случайным образом выбирается b_i, i=1, …, n;

- ∀i выбирается c_i так, чтобы b_ix₀+c_i=a_i.

После выполнения сервером необходимых операций клиент получает результирующий полином одной переменной. В результирующий полином подставляется значение х₀. Результат вычисляется с использованием схемы Горнера. Следует учесть, что вычисление значения полинома в точке является дешифровкой. В поле для отображения пользователю выводится результат, равный значению выражения.

Согласно варианту осуществления, работа сервера организована следующим образом. Многопоточный сервер находится в ожидании запроса клиента. Число обслуживаемых клиентов может быть ограничено с использованием специальных параметров. Каждый клиентский запрос обрабатывается в отдельном потоке. Сервер получает объект, содержащий набор переменных, зашифрованных соответствующими полиномами, а также функции, представленные строками.

Затем выполняется синтаксический анализ выражения с использованием метода рекурсивного спуска. Частные задачи с низким приоритетом освобождают управление для частных задач с высоким приоритетом. Приоритеты задач соответствуют приоритетам математических операций (то есть 1 - функции, 2 - выражения в скобках, 3 - вычисление экспоненциальных функций (возведение в степень), 4 - умножение и деление, 5 - сложение и вычитание).

В ходе вычисления функция и переменные заменяются соответствующими полиномами. Результат в виде полинома одной переменной передается клиенту. В случае вычисления экспоненциальной функции выражение для экспоненты вычисляется в первую очередь и передается клиенту. Клиент находит числовое значение экспоненты, повторно шифрует выражение и отправляет набор полиномов на сервер.

Следует учитывать, что гомоморфное шифрование может использоваться для шифрования серийных номеров программных компонентов и приложений. Например, разработчик приложения действует как клиент. Тогда для особого компонента, выступающего в роли сервера, формируется секретный ключ для проверки серийного номера приложения. Приложение, установленное на стороне конечного пользователя, получает серийный номер и проверяет его путем запуска специального алгоритма, использующего для анализа секретный ключ и предоставленный ключ. Поскольку секретный ключ недоступен приложению, то операции с этим ключом по проверке ключа серийного номера выполняются с гомоморфным шифрованием. Таким образом, взломщик программного обеспечения не может восстановить ключ, используя программу-отладчик или иные средства обратного инжиниринга. Поэтому взломщик программного обеспечения не сможет разработать программу-генератор ключей (кейген).

Серийный номер может быть проверен следующим образом. Во-первых, серийный номер может быть уже зашифрован (значением клиентской переменной), что используется алгоритмом на стороне сервера. Подобный алгоритм может использовать порядковый номер ключа совместно с контрольной суммой. Для обеспечения устойчивости к силовому взлому совокупное значение ключа и контрольной суммы должно иметь достаточную длину (4, 6 или 8 байт).

Далее, указанное значение шифруется гомоморфным ключом и передается на сервер. Сервер проверяет целостность контрольной суммы. Следует учитывать, что это значение дешифруется сервером, и достоверность серийного номера подтверждается. Для того, чтобы осуществить взлом, должна быть взломана процедура гомоморфного шифрования, что практически невозможно. Следует учитывать, что результат не зависит от того, где он вычисляется, поскольку результат использует предоставленный серийный номер и скрытую (внутреннюю) команду верификации контрольной суммы.

Первая реализация используется, если задействованы какие-либо уникальные данные приложения (например, регистрационный номер, идентификационный номер аппаратного обеспечения, адрес электронной почты пользователя, имя пользователя и т.д.). Эти уникальные данные задаются в текстовом виде компоненту, который выступает в роли сервера. В данном случае может применяться описанный выше способ вовлечения текстовых данных в вычисления на сервере. Альтернативный вариант состоит в том, что указанные данные (то есть идентификационные номера компонентов аппаратного обеспечения, контрольные суммы, имена пользователей и т.д.) могут отправляться на сервер регистрации и объединяться там с уникальным серийным номером версии, который содержит не только некоторый номер, но и производную от данных пользователя. Затем выполняется описанная выше процедура.

Следует учесть, что гомоморфное преобразование применяется только к тем частям вычислений, в которых требуется выполнить математические операции. Например, запись в базе данных может содержать два числовых и три строковых поля. Гомоморфное преобразование применяется для дешифровки числовых полей для последующего использования и ранжирования. Строковые поля могут шифроваться с использованием любого ключа, в том числе, ключа, который дает различные результаты для одних и тех же шифруемых данных.

Результат преобразования может также шифроваться перед передачей от сервера к клиенту, а также может соответствовать требованиям гомоморфного шифрования. Иными словами, предпочтительно, чтобы векторы исходных данных, функции и их суперпозиции также соответствовали гомоморфизму.

Простой пример объединения данных: формирование упорядоченного списка из некоторого числа зашифрованных данных. Каждому элементу списка назначается порядковый номер в зашифрованной форме, что является результатом выполнения операций на сервере.

Вариант осуществления также может быть реализован как операции на поле Галуа. В предложенном способе могут проводиться вычисления (умножение и сложение) на поле Галуа G(128) для оперирования с полиномами, используемыми в полностью гомоморфном шифровании.

Согласно варианту осуществления, используется конечное множество исходных числовых элементов. К числовому элементу применяется конечное множество операций, так что результат применения операции к любому набору элементов принадлежит тому же конечному множеству исходных элементов. Следует учитывать, что обычные арифметические умножение и сложение не соответствуют указанному условию, поскольку результат этих операций может не принадлежать к указанному конечному множеству числовых элементов. В связи с этим элементы поля Галуа используются в качестве исходных элементов, а операции умножения и сложения выполняются по правилам, принятым для поля Галуа.

Согласно варианту осуществления, конечный набор исходных элементов преобразуется (шифруется) в набор зашифрованных элементов, так что каждому зашифрованному элементу соответствует единственный исходный элемент. Результат операции над любой парой зашифрованных элементов формирует результирующий зашифрованный элемент, принадлежащий множеству зашифрованных элементов. Согласно одному из вариантов осуществления, операция сложения на поле Галуа требует сложения и (или)/умножения и (или) снижения степени полинома.

Иными словами, в схеме гомоморфного шифрования каждая операция над зашифрованными элементами соответствует только одной операции над исходными (незашифрованными) элементами, формирующей исходный результирующий элемент, соответствующий результирующему зашифрованному элементу. Согласно варианту осуществления, на стороне клиента формируется множество исходных элементов. Затем множество исходных элементов преобразуется во множество зашифрованных элементов.

Далее над зашифрованными элементами выполняются операции, в результате которых формируются результирующие зашифрованные элементы. Затем выбираются элементы исходного множества, соответствующие результирующим зашифрованным элементам. Согласно одному из вариантов осуществления, исходные элементы преобразуются в зашифрованные элементы первым алгоритмом шифрования (с использованием ключа шифрования). Затем обратное преобразование использует первый алгоритм дешифрования (применяется первый ключ дешифрования). Затем N-я операция над двумя зашифрованными элементами формирует результат, который может быть преобразован в исходный элемент N-ым алгоритмом дешифрования с использованием первого ключа дешифрования.

Альтернативный вариант заключается в том, что N-й алгоритм дешифрования требует дополнительный ключ дешифрования, отличающийся от первого ключа. Согласно одному из вариантов осуществления, криптосхема гомоморфного шифрования использует полином шифрования h(x)=ξ+(x-λ)r(x), где r(x) - произвольный полином из поля Галуа G(2ⁿ)[x]. Следует учесть, что матрица полинома имеет нулевой делитель и малый диапазон значений d/2, если степень полинома шифрования - d. Диапазон не зависит от произвольной степени полинома. В гомоморфном шифровании перемножение полиномов не увеличивает степень полиномов шифрования при условии использования полиномов из кольца Галуа.

В одном из вариантов осуществления могут использоваться элементы поля Галуа в виде простых чисел или в виде векторов в одномерной системе координат. Следует учитывать, что сложение или умножение векторов выполняется по модулю (то есть без учета направления), что позволяет результату оставаться в пределах выбранного кольца Галуа.

Если операции с полиномами требуют большого числа умножений или эквивалентных операций, то степень результирующих полиномов значительно возрастает, что делает затруднительным использование описанной концепции для формирования открытого и закрытого ключей на серверной стороне. Для преодоления указанного недостатка формируется полином с(x) степени d+1, причем в секретной точке z₀ значение c(z)=0. Полином с(x) становится открытым ключом и передается на сервер. В таком случае любое перемножение полиномов на сервере выполняется по модулю с(x), поэтому возрастания степени полиномов не происходит. Для формирования такого полинома достаточно выбрать любой полином w(x) степени d, тогда с(x)=w(x)(x-z₀).

В общем для противодействия возрастанию степени полином при зашифрованном умножении предлагается следующая процедура. Выберем полином s(x) ∈ GF(2ⁿ)[x]. Предположительно полином может быть разложен на значительное число простых сомножителей. В простейшем случае это линейные сомножители: s(x)=(x-λ₁)(x-λ₂)…(x-λ_p)r(x), где r(x) - произвольный полином. Элементы λ₁, λ₂, …, λ_p ∈ GF(2ⁿ) выбираются случайным образом. Таким образом, s(λ_i)=0, i=1, 2, …, p.

Рассмотрим кольцо GF(2ⁿ)[x]/s(x). Выберем секретный элемент λ₀ из множества λ₀ ∈ {λ₁, λ₂, …, λ_p}. Для любой пары ξ₁, ξ₂ ∈ GF(2ⁿ) выберем два полинома h₁(x), h₂(x) ∈ GF(2ⁿ)[x]/s(x) так, чтобы h₁(λ₀)=ξ₁, h₂(λ₀)=ξ₂. Перемножение полиномов выполняется в кольце GF(2ⁿ)[x]/s(x), в связи с чем степень произведения не возрастает. Произведение имеет вид h₁(x)h₂(x)=u(x)s(x)+ν(x).

В связи с этим в кольце GF(2ⁿ)[x]/s(x) произведение h₁(x)h₂(x)=ν(x). С другой стороны, в точке λ₀ получаем h₁(λ₀)h₂(λ₀)=u(λ₀)s(λ₀)+ν(λ₀)=ν(λ₀), поскольку s(λ₀)=0.

Таким образом, ξ₁ξ₂=h₁(λ₀)h₂(λ₀)=ν(λ₀). Степень полинома ν(x) не выше, чем степень полиномов h₁(x), h₂(x).

Требуется отправить на сервер полином s(x) вместе с данными. Для сокращения n можно модифицировать описанную конструкцию. Обратимся вновь к кольцу GF(2ⁿ)[z], в котором выбран исходный полином w(z). Рассмотрим подмножество R(z) полиномов из кольца GF(2ⁿ)[z], такое, что ƒ(z) ∈ R(z), если и только если ƒ(z)=αmod(w(z)), где α - произвольный элемент GF(2ⁿ). Множество R(z) является кольцом, и любой элемент ƒ(z) ∈ R(z) может быть представлен как ƒ(z)=g(z)w(z)+α. Следует учесть, что предыдущее условие соответствует случаю, когда w(z)=z-θ.

Рассмотрим множество элементов λ₁, λ₂, λ₃, …, λ_p ∈ GF(2ⁿ), на котором требуется выполнить зашифрованные операции. Для шифрования элементов используется множество полиномов ƒ_i(z)=g_i(z)w(z)+λ_i, i=1, 2, …, p. Полиномы передаются на сервер. Поскольку R(z) является кольцом, то вычисления будут выполняться корректно, и шифрование является гомоморфным.

Однако такая конструкция имеет недостаток, связанный с возрастанием степени полиномов. Для преодоления недостатка выберем унитарный полином u(z) той же степени, что и w(z). Может быть сформирован полином s(z)=u(z)w(z). Затем все вычисления выполняются на кольце GF(2ⁿ)[z]/s(z). Чтобы показать, что все вычисления верны, рассмотрим умножение двух элементов λ₁ и λ₂ на поле Галуа. Соответствующими шифрующими полиномами будут являться ƒ₁(z)=g₁(z)w(z)+λ₁ и ƒ₂(z)=g₂(z)w(z)+λ₂. Произведение этих полиномов на кольце GF(2ⁿ)[z]/s(z) имеет вид: h(z)=ƒ₁(z)f₂(z)mod(s(z)). С использованием китайской теоремы об остатках для вычисления ƒ₁(z)ƒ₂(z)mod(s(z)) достаточно вычислить ƒ₁(z)ƒ₂(z)mod(u(z)) и ƒ₁(z)ƒ₂(z)mod(w(z)). Поскольку полиномы u(z) и w(z) имеют одинаковую степень, то вычисление корректно. С другой стороны,

ƒ₁(z)ƒ₂(z)mod(w(z))=(g₁(z)w(z)+λ₁)(g₂(z)w(z)+λ₂)mod(w(z))=γ₁XORγ₂.

Из этого следует, что h(z)mod(w(z))=γ₁XORγ₂. Поэтому если сервер возвращает полином h(z), то по нему может быть восстановлен результат произведения без вычисления корня.

Описанный в настоящей заявке подход применим во многих ситуациях, в которых от сервера или сервиса облачных вычислений требуется выполнить вычисления с использованием данных без их дешифровки. Например, такой подход применим для операций с базами данных. Подход применим для операций по верификации банковских счетов. Пусть пользователь имеет банковский счет в банке А и банковский счет в банке В. Оба банка направляют в зашифрованной форме балансы в сервис облачных вычислений, где в зашифрованной форме выполняется гомоморфное суммирование, в результате чего для третей стороны формируется результат. Таким образом, третья сторона получит информацию о суммарном балансе по счетам А и В, однако баланс по каждому из счетов в отдельности останется для третей стороны неизвестным.

Одно из достоинств некоторых вариантов осуществления, описанных в настоящей заявке, состоит в том, что вычисления на полях Галуа GF(2ⁿ) могут эффективно выполняться на аппаратном уровне. Например, сумма элементов поля Галуа выполняется с помощью операции "исключающее или", которая на большинстве процессоров выполняется за один такт. Также вычисления на поле Галуа никогда не приводят к ошибкам (неприемлемый результат, переполнение буфера и т.п.). Кроме того, предложенный подход устойчив к атакам на основе подбора ключа.

На фиг. 1 показан пример структурной схемы системы для реализации изобретения. Система содержит вычислительное устройство общего назначения в виде персональной электронно-вычислительной машины (ПЭВМ) или сервера 20 или подобного вычислителя, содержащего вычислительное устройство 21, системное запоминающее устройство 22 и системную шину 23, которая объединяет различные компоненты системы, в том числе, системное запоминающее устройство 22 и вычислительное устройство 21. Системная шина 23 может быть шиной любого типа, в том числе, шиной запоминающего устройства или контроллером запоминающего устройства, периферийной шиной, локальной шиной, и быть построена по любой архитектуре шин. В состав системного запоминающего устройства сходят постоянное запоминающее устройство (ПЗУ) 24 и оперативное запоминающее устройство (ОЗУ) 25. В ПЗУ 24 хранится базовая система ввода-вывода 26, которая содержит базовые процедуры, способствующие передаче информации между составными частями ПЭВМ 20, в частности, во время начальной загрузки.

ПЭВМ 20 может также содержать: накопитель 27 на жестких дисках для чтения и записи информации на жесткие диски (на фиг. 1 сами жесткие диски условно не показаны); привод 28 магнитных дисков для чтения и записи информации на сменные магнитные диски 29; привод 30 оптических дисков для чтения и записи информации на сменные оптические диски 31, такие, как CD-ROM (от английского Compact disk read-only memory - компакт-диск - постоянное запоминающее устройство), DVD-ROM (от английского Digital video disc read-only memory - цифровой видеодиск - постоянное запоминающее устройство) или оптические машиночитаемые среды другого типа. Накопитель 27 на жестких дисках, привод 28 магнитных дисков и привод 30 оптических дисков подключены к системной шине 23 с помощью интерфейса 32 накопителя на жестких дисках, интерфейса 33 привода магнитных дисков и интерфейса 34 привода оптических дисков соответственно.

Приводы и соответствующие машиночитаемые среды обеспечивают ПЭВМ 20 энергонезависимое хранение машиночитаемых инструкций, структур данных, программных модулей и подпрограмм, которые могут использоваться для реализации этапов описанного в настоящей заявке способа, а также хранения прочих данных.

Несмотря на то, что в описываемом варианте осуществления используется жесткий диск, магнитный диск 29 и сменный оптический диск 31, специалистам в данной области должно быть понятно, что для хранения данных, доступных ПЭВМ, могут использоваться машиночитаемые среды других типов, в частности, магнитные кассеты, карты флэш-памяти, цифровые видеодиски, картриджи для накопителей Бернулли, накопители на ОЗУ и ПЗУ и т.п.

Некоторое число программных модулей может храниться на жестком диске, магнитном диске 29, оптическом диске 31, ПЗУ 24 или ОЗУ 25, в том числе, операционная система 35 (например, "Windows 2000"). ПЭВМ 20 содержит: файловую систему 36, связанную или входящую в состав операционной системы 35, такую, как Windows NTFS (от английского New technology file system - файловая система новой технологии); одну или более прикладных программ 37; другие программные модули 38; данные 39 программ. Пользователь может вводить команды и информацию в ПЭВМ 20 через устройства ввода, такие, как клавиатура 40 и указывающее устройство 42.

В состав прочих устройств ввода (на фиг. 1 не показаны) могут входить: микрофон; джойстик; игровой пульт управления; спутниковая антенна; сканер; другие подобные устройства. Перечисленные и прочие устройства ввода обычно соединяются с процессорным устройством 21 через интерфейс 46 последовательного порта, который подключается к системной шине. Однако указанные устройства ввода могут подключаться и через другие интерфейсы, такие, как параллельный порт, игровой порт, порт USB (от английского Universal serial bus - универсальная последовательная шина). Также к системной шине 23 через интерфейс, такой, как видеоадаптер 48, подключается монитор 47 или устройство другого типа для отображения видеоинформации. Помимо монитора 47 персональные ЭВМ обычно содержат другие периферийные устройства вывода, такие, как громкоговорители и принтеры.

ПЭВМ 20 может действовать в сетевом окружении с использованием логических подключений к одному или более удаленных компьютеров 49. Удаленным компьютером (компьютерами) 49 могут быть: другая ПЭВМ; сервер; роутер; сетевая ПЭВМ; сетевое устройство, напрямую взаимодействующее с другими устройствами в сетевом окружении; другой узел той же сети. Кроме того, удаленный компьютер 49 обычно содержит многие или все функциональные узлы, описанные выше применительно к ПЭВМ 20, хотя для него показано только запоминающее устройство 50. В число логических подключений входят локальная вычислительная сеть (ЛВС) 51 и глобальная вычислительная сеть 52. Описанное сетевое окружение распространено в офисах, вычислительных сетях предприятий, сетях интранет и интернет.

При использовании в сетевом окружении ЛВС ПЭВМ 20 подключена к ЛВС 51 через сетевой интерфейс (сетевой адаптер) 53. При использовании в сетевом окружении глобальной вычислительной сети ПЭВМ 20 обычно содержит модем 54 или иное средство установления соединения через глобальную вычислительную сеть 52, такую, как интернет. Модем 54, который может быть внутренним или внешним, подключается к системной шине 23 через интерфейс 46 последовательного порта.

В сетевом окружении программные модули, изображенные относительно ПЭВМ 20 или его частей, могут храниться во внешнем по отношению к ПЭВМ 20 (удаленном) запоминающем устройстве. Следует учитывать, что показанные сетевые подключения служат в качестве примера, и могут использоваться другие средства установления коммуникационного соединения между компьютерами.

Компьютеры, подобные описанным выше, могут применяться к обычных вычислительных сетях, например, интернет, ЛВС, региональных сетях, глобальных сетях и т.д. Перечисленные сети могут объединять различные ресурсы, в число которых входят компьютеры пользователей, серверы, поставщики интернет-услуг, телефонные аппараты, соединенные с сетью и т.д.

Таким образом, с учетом приведенного описания предпочтительных вариантов осуществления, специалистам в данной области должно быть понятно, что описанный способ и система обладают определенными преимуществами. Также должно быть понятно, что в рамках настоящего изобретения могут быть выполнены различные модификации, адаптации и альтернативные варианты осуществления. Изобретение определяется следующей формулой изобретения.