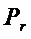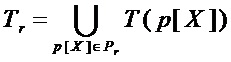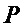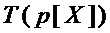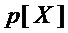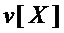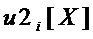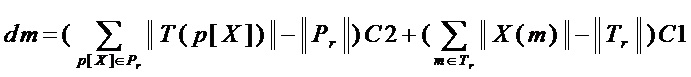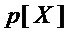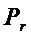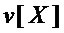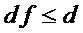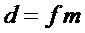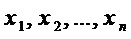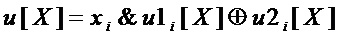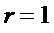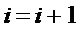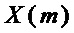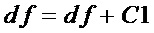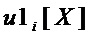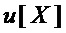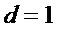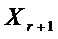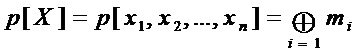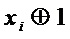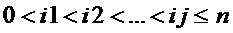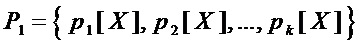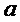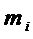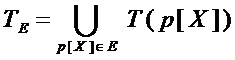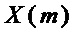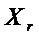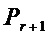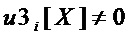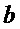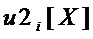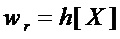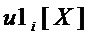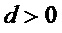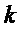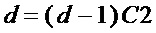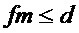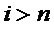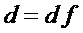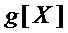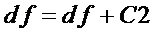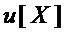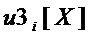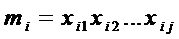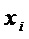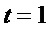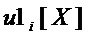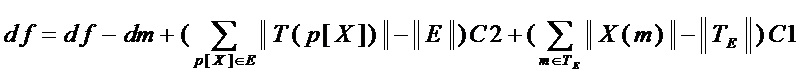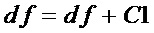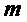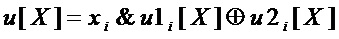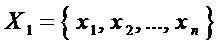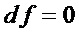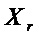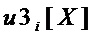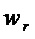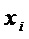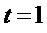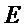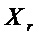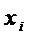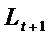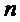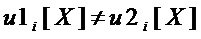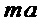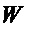Результат интеллектуальной деятельности: Способ формирования S-блока
Вид РИД
Изобретение
Область техники, к которой относится изобретение
Предполагаемое изобретение относится к области обработки информации и криптографии и, в частности, к способам формирования S-блоков замены с минимальным количеством логических элементов, для последующего использования в аппаратуре систем обработки данных и криптографической защиты информации.
Уровень техники
Операции замены 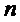 -битовых двоичных векторов на
-битовых двоичных векторов на 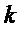 -битовые двоичные вектора, реализуемые в блоках замены (S-блоках), широко используются для криптографического преобразования данных, для сжатия информации и/или защиты от помех при хранении и при передаче информации по каналам связи.
-битовые двоичные вектора, реализуемые в блоках замены (S-блоках), широко используются для криптографического преобразования данных, для сжатия информации и/или защиты от помех при хранении и при передаче информации по каналам связи.
Способы формирования S-блоков с минимальным количеством логических элементов известны и зависят от состава логических элементов схемотехнической реализации.
Так, для набора логических элементов, реализующих логические операции И (&), ИЛИ (V), НЕ (¬), известны метод Квайна-МакКласки, алгоритм Блейка – Порецкого и др. [1]. Однако, известные методы предназначены для оптимизации одной булевой функции, а не набора из 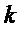 булевых функций, задающих S-блок. Кроме того, эти методы неприменимы к набору логических элементов, реализующих логические операции & и XOR (⊕, исключающее ИЛИ).
булевых функций, задающих S-блок. Кроме того, эти методы неприменимы к набору логических элементов, реализующих логические операции & и XOR (⊕, исключающее ИЛИ).
Известен способ минимизации булевой функции для набора логических элементов {&, ⊕}, предложенный как составная часть процесса запоминания цифровой информации [2]. Однако, этот способ также предназначен для минимизации только одной булевой функции и не учитывает возможности совместной оптимизации нескольких булевых функций, представляющих S-блок. При этом, в данном способе оптимизируется суммарное число элементов & и ⊕ и не принимается во внимание, что схемотехнические затраты на реализацию операций & и ⊕ могут существенно отличаться друг от друга.
Наиболее близким по своей технической сущности к заявляемому является известный способ эффективной реализации S-блока, используемого в стандарте криптографической защиты информации AES [3], в котором, наряду с оптимизацией времени вычисления S-блока, решается и задача минимизации числа логических элементов {&, ⊕} при реализации данного S-блока.
Известный способ [3] выбирается в качестве прототипа.
Основным недостатком прототипа является то, что он предназначен исключительно для S-блоков частного вида, а именно, для S-блоков, задаваемых несколькими (небольшим числом) операций в конечном поле 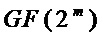 , к которым и относиться S-блок стандарта криптографической защиты AES. Прототип непосредственно опирается на реализацию операции умножения в конечном поле
, к которым и относиться S-блок стандарта криптографической защиты AES. Прототип непосредственно опирается на реализацию операции умножения в конечном поле 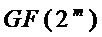 , поэтому он неприменим к произвольному S-блоку, не основанному на какой-либо алгебраической системе.
, поэтому он неприменим к произвольному S-блоку, не основанному на какой-либо алгебраической системе.
Другим недостатком (ограничением) прототипа является то, что он осуществляет минимизацию числа логических элементов {&, ⊕} для реализации S-блока в несколько тактов/шагов (для итеративной схемы реализации). При этом число итераций при вычислениях S-блока возрастает с увеличением размера m конечного поля 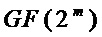 .
.
Раскрытие изобретения
Техническим результатом предлагаемого способа является
1) уменьшение схемотехнических затрат при реализации S-блока с помощью логических элементов & и ⊕,
2) возможность учета различных схемотехнических затрат на реализацию элементов & и ⊕ в процессе минимизации результирующей логической схемы S-блока.
В заявленном способе также отсутствуют ограничения на значения 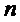 и
и 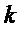 размерности S-блока.
размерности S-блока.
S-блок осуществляет замену входного двоичного вектора 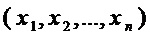 длины
длины 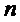 на выходной двоичный вектор
на выходной двоичный вектор 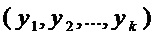 длины
длины 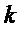 , где
, где 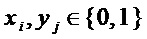 для
для 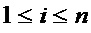 и
и 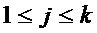 .
.
S-блок однозначно задается аналитически координатными булевыми функциями 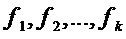 от
от 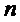 переменных
переменных 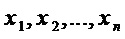 , что можно записать в виде
, что можно записать в виде
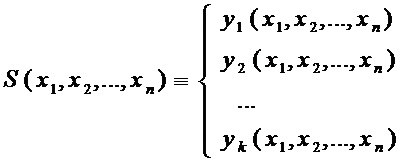
В предлагаемом способе рассматривается представление координатных булевых функций S-блока через приведенные многочлены Жегалкина: каждая функция 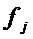 для
для 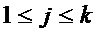 аналитически задана в виде
аналитически задана в виде
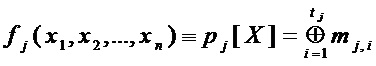
где 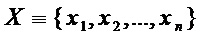 – множество переменных многочленов
– множество переменных многочленов 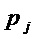 ,
, 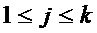 ;
;
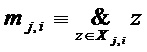 - моном многочлена
- моном многочлена 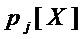 , который является произведением всех переменных
, который является произведением всех переменных 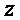 из подмножества
из подмножества 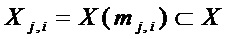 множества
множества 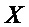 , причем
, причем 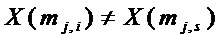 при
при 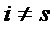 для приведенного многочлена
для приведенного многочлена 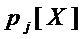 .
.
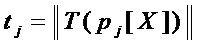 - мощность (число элементов) множества
- мощность (число элементов) множества 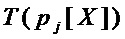 - мономов
- мономов 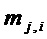 , составляющих многочлен
, составляющих многочлен 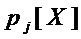 .
.
Существуют и другие, отличные от приведенного многочлена Жегалкина, формы представления булевых функций, например: таблица истинности, дизъюнктивная нормальная форма (ДНФ), конъюнктивная нормальная форма (КНФ). Процессы перехода от одного вида представления к другому хорошо известны. Например, в известном способе [4] приведена последовательность перехода от таблицы истинности к представлению булевой функции через приведенный многочлен Жегалкина. В заявляемом способе не имеет значения, каким образом формируется исходное аналитическое представление S-блока через приведенные многочлены Жегалкина:
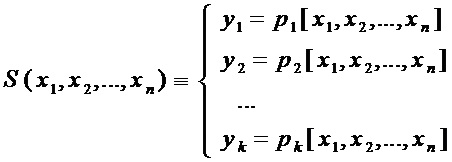
Для построения оптимальной логической схемы реализации S-блока через операции & и ⊕ в заявляемом способе используются предварительные аналитические вычисления, использующие операции над множествами. Для получаемого в результате схемотехнического решения не имеет значения, какие используются представления множеств (характеристический вектор, список элементов, в том числе упорядоченный список, и т.д.) и с помощью каких преобразований осуществляются операции над множествами.
Прямой способ реализации S-блока (1), заданного множеством приведенных многочленов Жегалкина 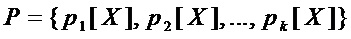 , состоит из двух этапов:
, состоит из двух этапов:
1. Составляют множество 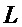 мономов, входящих в состав многочленов из множества
мономов, входящих в состав многочленов из множества 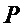 , по формуле
, по формуле
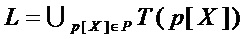 ,
,
где 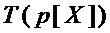 – множество мономов, составляющих многочлен
– множество мономов, составляющих многочлен 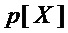 .
.
Каждый моном 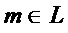 реализуют через конъюнкцию & всех элементов множества
реализуют через конъюнкцию & всех элементов множества 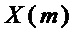 - подмножества множества
- подмножества множества 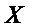 входных переменных S-блока, где
входных переменных S-блока, где 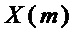 – множество переменных монома
– множество переменных монома 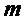 .
.
2. Каждый многочлен 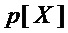 из множества
из множества 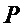 реализуют, как сумму ⊕ выходов из схем реализаций мономов
реализуют, как сумму ⊕ выходов из схем реализаций мономов 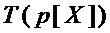 , полученных на предыдущем этапе.
, полученных на предыдущем этапе.
В этом способе схема реализации монома 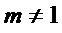 (свободному члену) требует
(свободному члену) требует 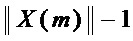 элементов &, где
элементов &, где 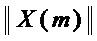 – мощность множества
– мощность множества 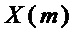 – множества переменных монома
– множества переменных монома 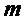 .
.
Аналогично, схема реализации многочлена 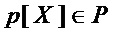 требует
требует 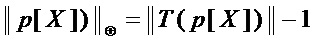 элементов ⊕, где
элементов ⊕, где 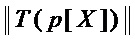 – мощность множества
– мощность множества 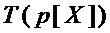 - множества мономов, составляющих многочлен
- множества мономов, составляющих многочлен 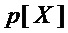 .
.
Тем самым, аддитивная сложность 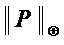 и мультипликативная сложность
и мультипликативная сложность 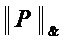 реализации множества многочленов
реализации множества многочленов 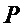 составляют:
составляют:
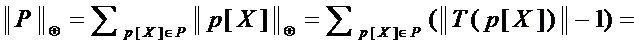
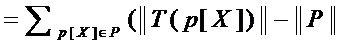 ,
,
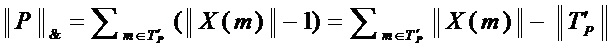 (1)
(1)
где 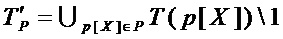 – множество мономов, входящих в состав многочленов множества
– множество мономов, входящих в состав многочленов множества 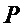 , за исключением свободного члена 1.
, за исключением свободного члена 1.
Если схемотехнические затраты на реализацию операции & составляют 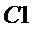 единиц, а затраты на реализацию операции ⊕ -
единиц, а затраты на реализацию операции ⊕ - 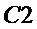 единиц, суммарные затраты
единиц, суммарные затраты 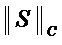 на реализацию S-блока составят
на реализацию S-блока составят
|
Заявляемый способ состоит из аналитического этапа, на котором выполняется последовательная декомпозиция исходных многочленов, задающих S-блок, на суммы и произведения более простых многочленов, для реализации которых требуется меньше суммарных схемотехнических затрат, этапа синтеза, на котором создаются схемы реализации этих, далее не упрощаемых, многочленов и на основе этих схем в порядке обратном декомпозиции строится итоговая логическая схема реализации S-блока, и третьего этапа, в ходе которого итоговая логическая схема реализуется в электронной схеме.
На каждом шаге декомпозицию множества многочленов осуществляют одним из двух следующих преобразований.
Преобразование 1 определяется парой многочленов 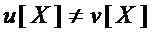 из рассматриваемого множества многочленов
из рассматриваемого множества многочленов 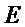 , и состоит из следующих вычислений:
, и состоит из следующих вычислений:
• выделяют множество 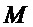 общих мономов многочленов
общих мономов многочленов 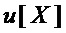 и
и 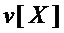
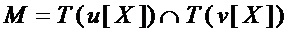
• вычисляют мощность 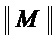 ;
;
• если 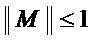 (это равносильно тому, что многочлены
(это равносильно тому, что многочлены 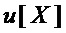 и
и 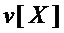 или не имеют общих мономов или имеют ровно один такой моном), то данное преобразование прекращают, так как оно не дает снижения схемотехнических затрат;
или не имеют общих мономов или имеют ровно один такой моном), то данное преобразование прекращают, так как оно не дает снижения схемотехнических затрат;
• если 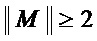 , то из мономов множества
, то из мономов множества 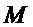 составляют многочлен
составляют многочлен 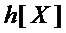 , а из мономов множеств
, а из мономов множеств 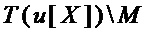 и
и 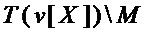 – многочлены
– многочлены 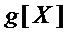 и
и 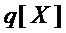 соответственно;
соответственно;
• вычисляют, в качестве декомпозиции многочленов 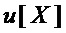 и
и 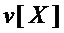 , соотношения
, соотношения
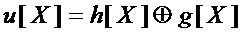 ,
,
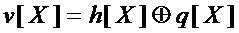 ,
,
в которых слагаемые, равные 0, обозначают, что операцию ⊕ реализовывать не требуется;
• формируют результирующее множество многочленов
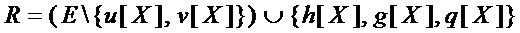
• вычисляют эффективность преобразования (величину уменьшения схемотехнических затрат) в виде
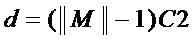
Преобразование 2 определяется параметром 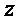 – переменной из множества
– переменной из множества 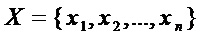 и состоит из следующих вычислений для каждого многочлена
и состоит из следующих вычислений для каждого многочлена 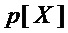 из рассматриваемого множества многочленов
из рассматриваемого множества многочленов 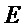 :
:
• для рассматриваемого многочлена 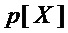 формируют множество
формируют множество 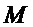 мономов, содержащих переменную
мономов, содержащих переменную 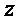
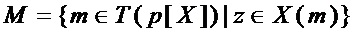
• вычисляют мощность 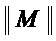 множества
множества 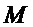 ;
;
• если 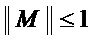 (это равносильно тому, что многочлен
(это равносильно тому, что многочлен 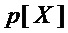 или не зависит от переменной
или не зависит от переменной 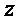 , или имеет ровно один моном, содержащий переменную
, или имеет ровно один моном, содержащий переменную 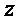 ), то
), то 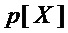 не подвергают декомпозиции, в неизменном виде включают в результирующее (формируемое) множество многочленов
не подвергают декомпозиции, в неизменном виде включают в результирующее (формируемое) множество многочленов 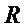 , а сложность его декомпозиции
, а сложность его декомпозиции 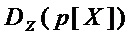 полагают равной нулю;
полагают равной нулю;
• если 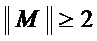 , то осуществляют декомпозицию многочлена
, то осуществляют декомпозицию многочлена 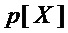 , выполняя следующие действия:
, выполняя следующие действия:
◯ из мономов множества 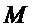 исключают переменную
исключают переменную 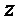 и формируют многочлен
и формируют многочлен 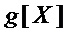
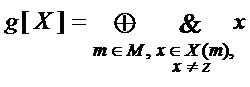 ,
,
причем моном 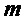 , состоящий из единственной переменной
, состоящий из единственной переменной 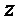 , переходит в свободный член 1 многочлена
, переходит в свободный член 1 многочлена 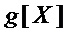 ;
;
◯ из мономов множества 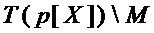 (мономов многочлена
(мономов многочлена 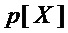 , не содержащих переменную
, не содержащих переменную 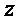 ) формируют многочлен
) формируют многочлен 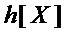
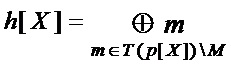
◯ вычисляют многочлен
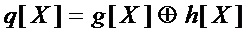
◯ приводят подобные члены в 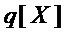 (исключают повторяющиеся мономы)
(исключают повторяющиеся мономы)
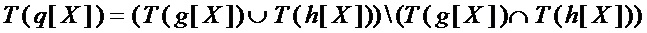
◯ если число мономов многочлена 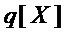 меньше числа мономов многочлена
меньше числа мономов многочлена 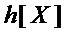 на 2 и более, что равносильно условию на мощности множеств
на 2 и более, что равносильно условию на мощности множеств
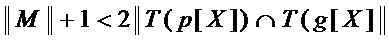 ,
,
то в качестве декомпозиции многочлена 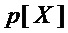 используют выражение
используют выражение
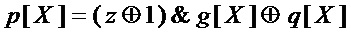 ,
,
▪ включают в результирующее множество многочленов 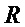 многочлены
многочлены 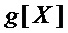 ,
, 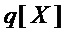 и
и 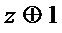 ;
;
▪ принимают значение сложности декомпозиции 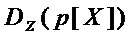 многочлена
многочлена 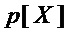 равной
равной 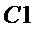 , если
, если 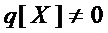 , то увеличивают значение
, то увеличивают значение 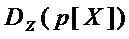 на
на 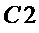
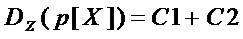 ;
;
◯ если же
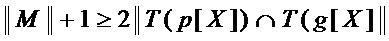 ,
,
то в качестве декомпозиции многочлена 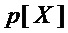 используют выражение
используют выражение
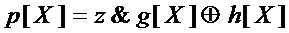 ,
,
▪ включают в результирующее (формируемое) множество многочленов 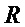 многочлены
многочлены 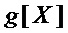 и
и 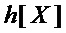 ;
;
▪ принимают значение сложности декомпозиции 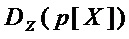 многочлена
многочлена 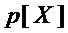 равной
равной 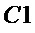 , если
, если 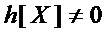 , то увеличивают значение
, то увеличивают значение 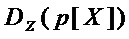 на
на 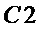
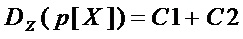
Эффективность преобразования 2 (величину уменьшения схемотехнических затрат) для рассматриваемого множества многочленов 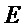 и переменной
и переменной 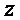 рассчитывают по формуле:
рассчитывают по формуле:
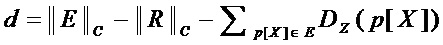 ,
,
где значения 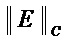 и
и 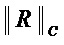 вычисляются по формулам (1) и (2).
вычисляются по формулам (1) и (2).
Для минимизации схемотехнических затрат на реализацию мономов из множества 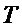 проводят разложение мономов
проводят разложение мономов 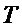 в произведение мономов с меньшим числом переменных, используя следующее преобразование.
в произведение мономов с меньшим числом переменных, используя следующее преобразование.
Преобразование 3 состоит из следующих вычислений и операций:
• осуществляют во множестве мономов 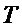 поиск для обнаружения пары мономов
поиск для обнаружения пары мономов 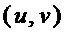 , причем
, причем 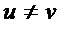 , с наибольшим числом общих переменных, путем последовательного перебора, то есть находят пару мономов с максимальным значением
, с наибольшим числом общих переменных, путем последовательного перебора, то есть находят пару мономов с максимальным значением
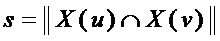
где 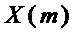 – множество переменных в мономе
– множество переменных в мономе 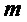
• если 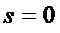 (это равносильно тому, что у мономов рассматриваемого множества
(это равносильно тому, что у мономов рассматриваемого множества 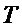 нет общих переменных), то завершают преобразование
нет общих переменных), то завершают преобразование
• если 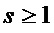 , то выполняют следующие действия:
, то выполняют следующие действия:
• составляют мономы 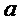 ,
, 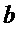 ,
, 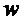 из переменных
из переменных 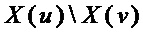 ,
, 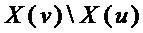 и
и 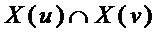 , соответственно; в качестве разложения мономов
, соответственно; в качестве разложения мономов 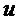 и
и 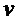 используют выражения
используют выражения
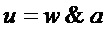 ,
,
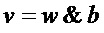 ,
,
в которых сомножители, равные 1, обозначают, что операцию & реализовывать не требуется;
• формируют результирующее множество мономов 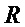 , удаляя из множества
, удаляя из множества 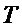 мономы
мономы 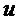 и
и 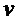 и добавляя мономы
и добавляя мономы 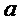 ,
, 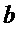 ,
, 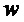 , т.е. вычисляют
, т.е. вычисляют
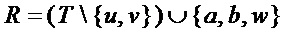
Предлагаемый способ минимизации схемотехнических затрат на реализацию S-блока, заданного многочленами Жегалкина 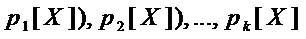 , состоит из 7 этапов.
, состоит из 7 этапов.
1. Исходное множество многочленов
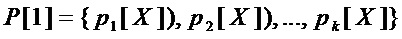
последовательно преобразовывают с использованием преобразований 1 и 2:
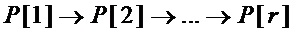
где каждый переход имеет эффективность больше нуля (т.е. приводит к снижению оценки суммарных схемотехнических затрат и осуществляется к результирующему множеству многочленов, формируемому в ходе этих преобразований). Результирующее множество 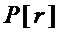 характеризуется тем, что никакое из преобразований 1 и 2 не приводит к дальнейшему снижению оценки затрат ни при каких параметрах.
характеризуется тем, что никакое из преобразований 1 и 2 не приводит к дальнейшему снижению оценки затрат ни при каких параметрах.
2. Затем, по результирующему множеству 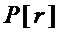 формируют множество мономов
формируют множество мономов 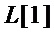 , входящих в многочлены множества
, входящих в многочлены множества 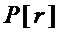 и добавляют к нему множество входных переменных
и добавляют к нему множество входных переменных 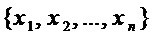
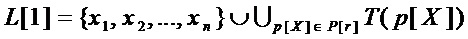 ,
,
где 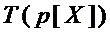 – множество мономов, составляющих многочлен
– множество мономов, составляющих многочлен 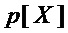 .
.
3. Затем осуществляют разложение мономов множества 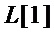 , многократно используя преобразование 3 до тех пор, пока преобразование станет неприменимым, и получают последовательность множеств
, многократно используя преобразование 3 до тех пор, пока преобразование станет неприменимым, и получают последовательность множеств
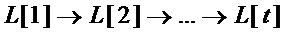
Поскольку переменные 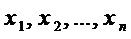 не удаляют в процессе преобразования множества мономов, то невозможность применения преобразования 3 к множеству
не удаляют в процессе преобразования множества мономов, то невозможность применения преобразования 3 к множеству 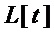 равносильно тому, что
равносильно тому, что 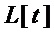 состоит только из элементов
состоит только из элементов 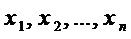 , которые и являются входами S-блока.
, которые и являются входами S-блока.
4. Построение логической схемы S-блока начинают проходом по цепочке 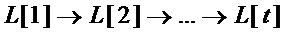 в обратном порядке, соединяя операцией & выходы схем мономов, участвующих в разложении, схемы которых, в свою очередь, были составлены на предыдущих шагах.
в обратном порядке, соединяя операцией & выходы схем мономов, участвующих в разложении, схемы которых, в свою очередь, были составлены на предыдущих шагах.
5. После построения логических схем мономов из множества 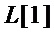 формируют логические схемы многочленов из множества
формируют логические схемы многочленов из множества 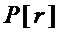 , соединяя операцией ⊕ выходы схем мономов
, соединяя операцией ⊕ выходы схем мономов 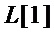 , составляющих этот многочлен.
, составляющих этот многочлен.
6. Далее осуществляют проход по цепочке 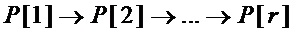 в обратном порядке, и составляют логические схемы очередных многочленов, соединяя операциями & и ⊕ выходы схем предшествующих многочленов в соответствии с формулами декомпозиции.
в обратном порядке, и составляют логические схемы очередных многочленов, соединяя операциями & и ⊕ выходы схем предшествующих многочленов в соответствии с формулами декомпозиции.
7. Выходы логических схем многочленов множества 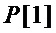 используют в качестве выходов логической схемы S-блока.
используют в качестве выходов логической схемы S-блока.
В описанном способе минимизации схемотехнических затрат не специфицированы параметры, которые используются для переходов 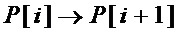 и
и 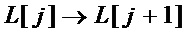 . Однако, от выбора этих параметров зависит получаемый эффект снижения схемотехнических затрат. Эффективный метод выбора наилучшего набора параметров, обеспечивающих наименьшее из возможных значений суммарных схемотехнических затрат, неизвестен, а полный перебор всех наборов требует экспоненциальных вычислительных затрат от величины
. Однако, от выбора этих параметров зависит получаемый эффект снижения схемотехнических затрат. Эффективный метод выбора наилучшего набора параметров, обеспечивающих наименьшее из возможных значений суммарных схемотехнических затрат, неизвестен, а полный перебор всех наборов требует экспоненциальных вычислительных затрат от величины 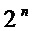 , что делает перебор неприемлемым для практически интересных значений
, что делает перебор неприемлемым для практически интересных значений 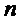 .
.
В заявляемом способе предлагается выбирать параметры перехода так, чтобы на каждом переходе 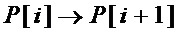 и
и 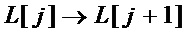 уменьшение оценки схемотехнических затрат было максимально возможным, а среди параметров, обеспечивающих такое снижение оценки, использовать параметры, запись (представление) которых предшествует записям остальным в лексикографическом порядке.
уменьшение оценки схемотехнических затрат было максимально возможным, а среди параметров, обеспечивающих такое снижение оценки, использовать параметры, запись (представление) которых предшествует записям остальным в лексикографическом порядке.
Необходимо отметить, что построение (формирование) логической схемы, реализующей соответствующую булеву функцию, является известным процессом (этот процесс описан, например, в [1, 4]).
Реализация электронной схемы на основе полученной логической схемы также является известным процессом и может быть выполнена как на дискретных элементах, так и с использованием интегральных микросхем, в том числе программируемых логических интегральных микросхем (ПЛИС), по выбору разработчика.
Краткое описание чертежей
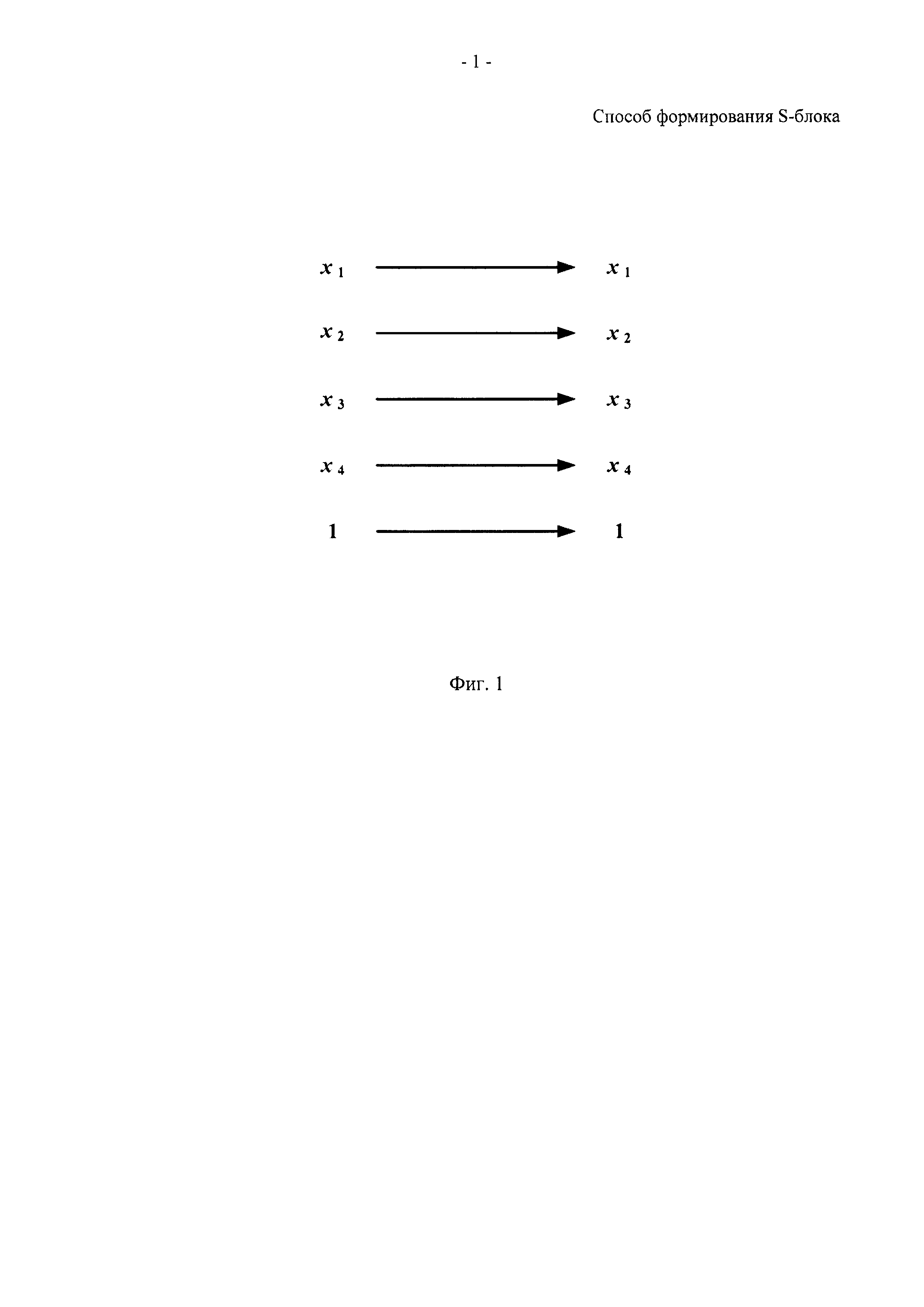
На фиг. 1 показана начальная логическая схема для примера реализации способа.
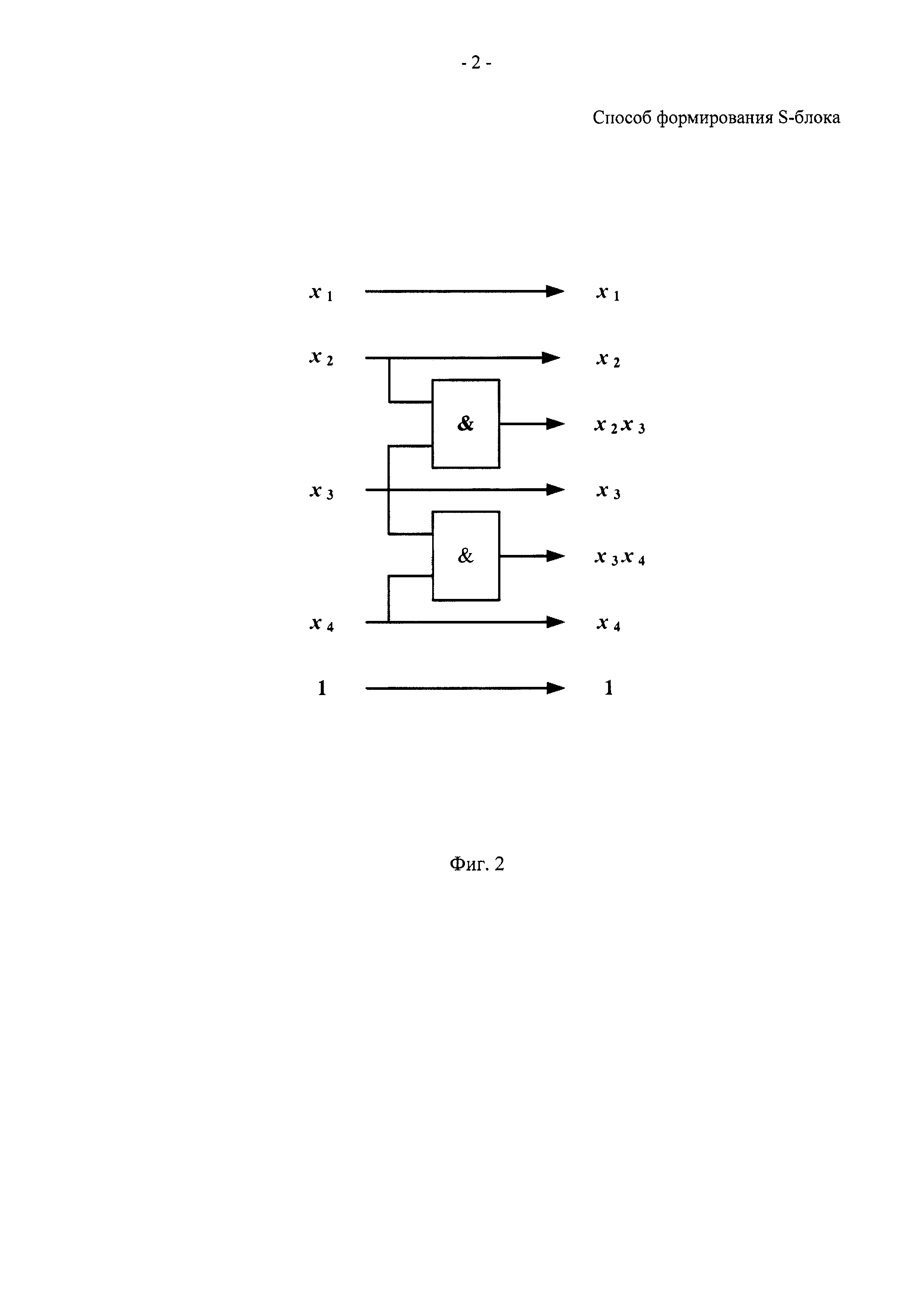
На фиг. 2 показана промежуточная логическая схема для примера реализации способа.
На фиг. 3 показана промежуточная логическая схема для примера реализации способа.
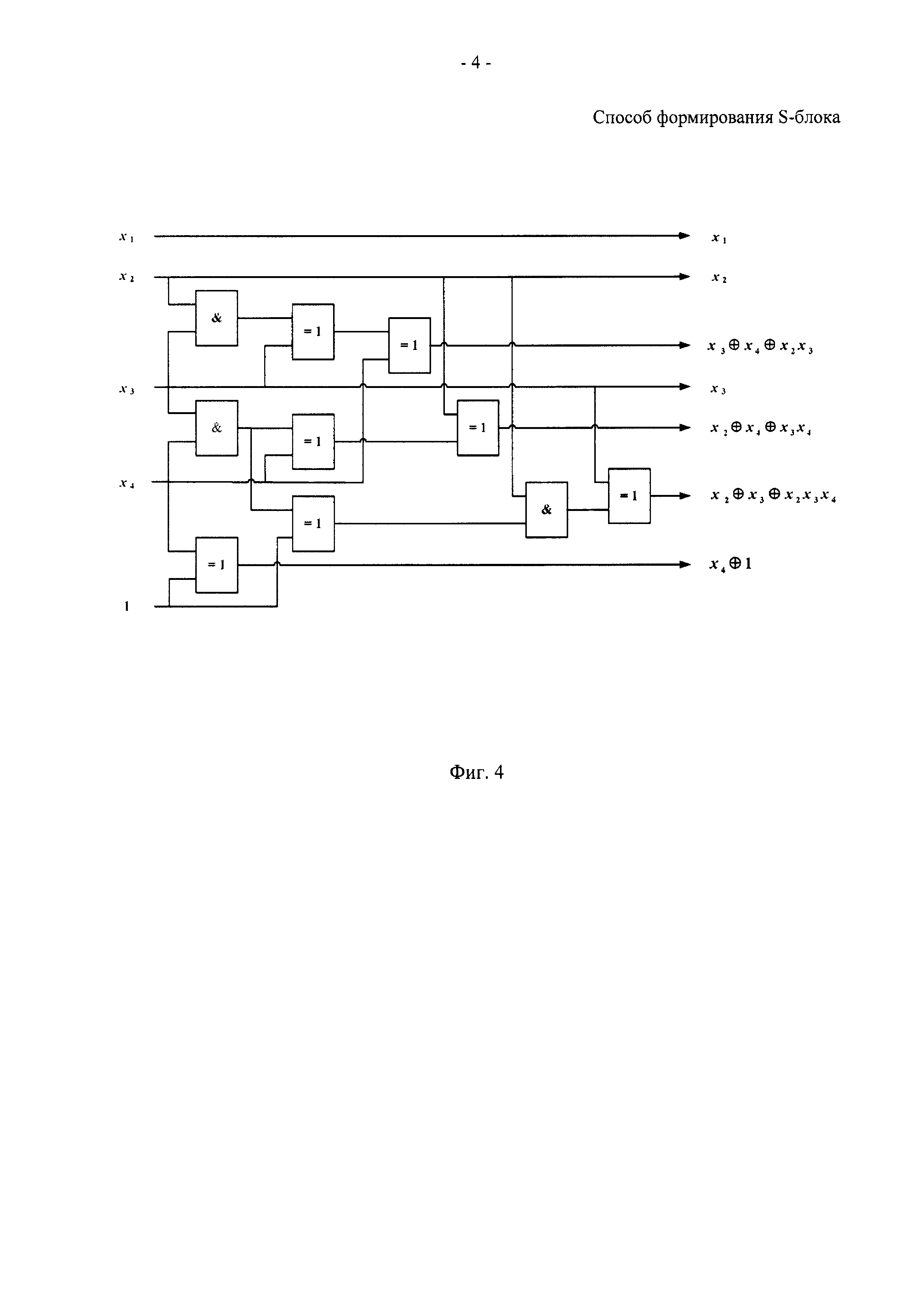
На фиг. 4 показана промежуточная логическая схема для примера реализации способа.
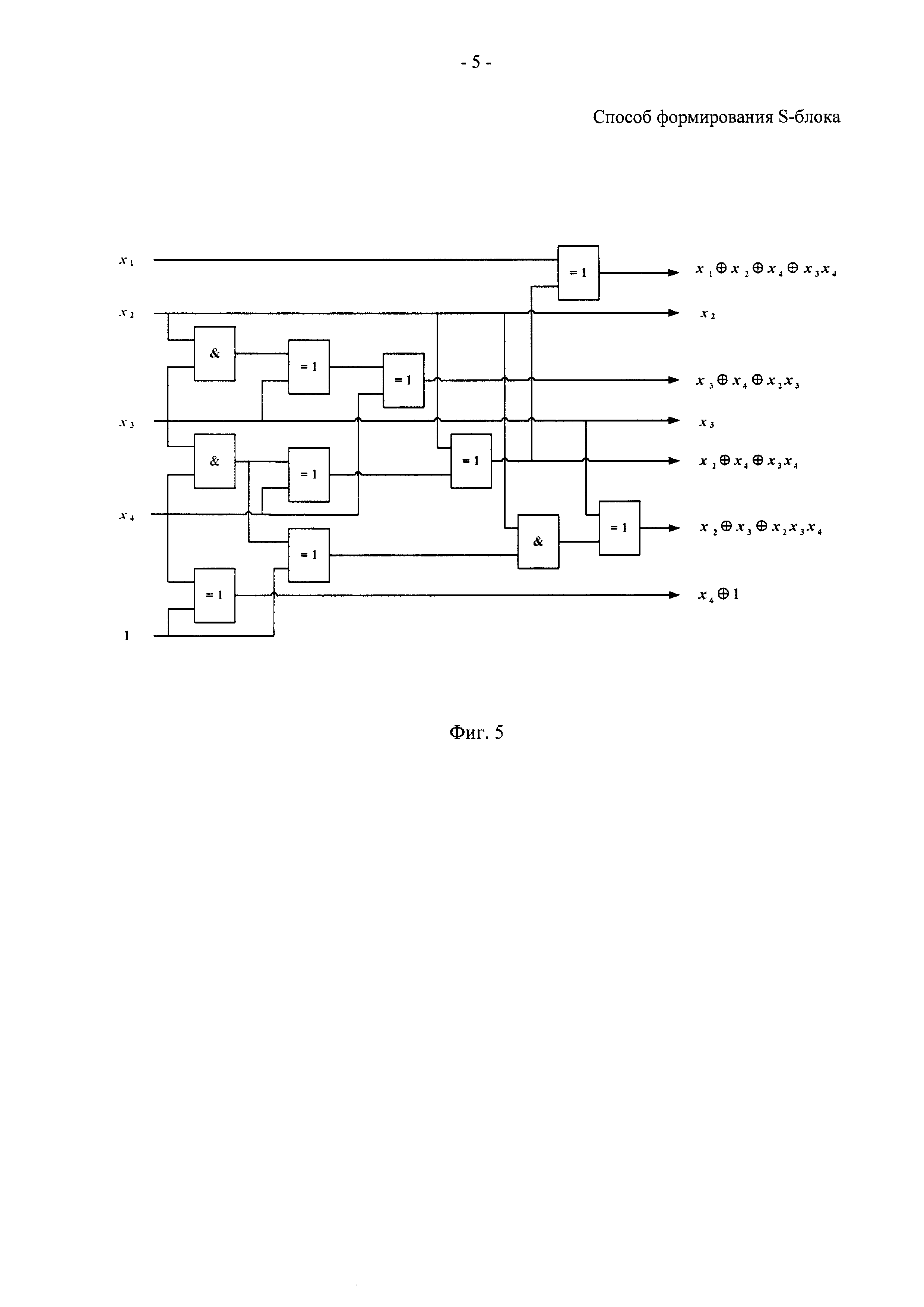
На фиг. 5 показана промежуточная логическая схема для примера реализации способа.
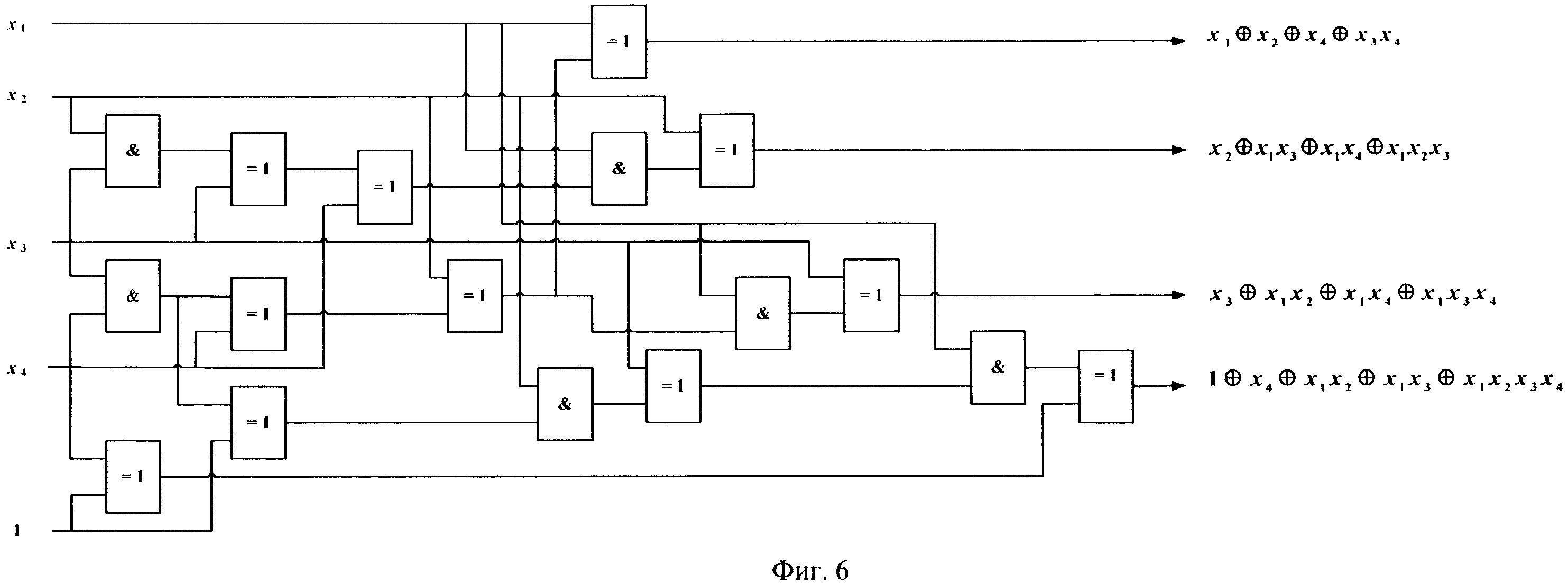
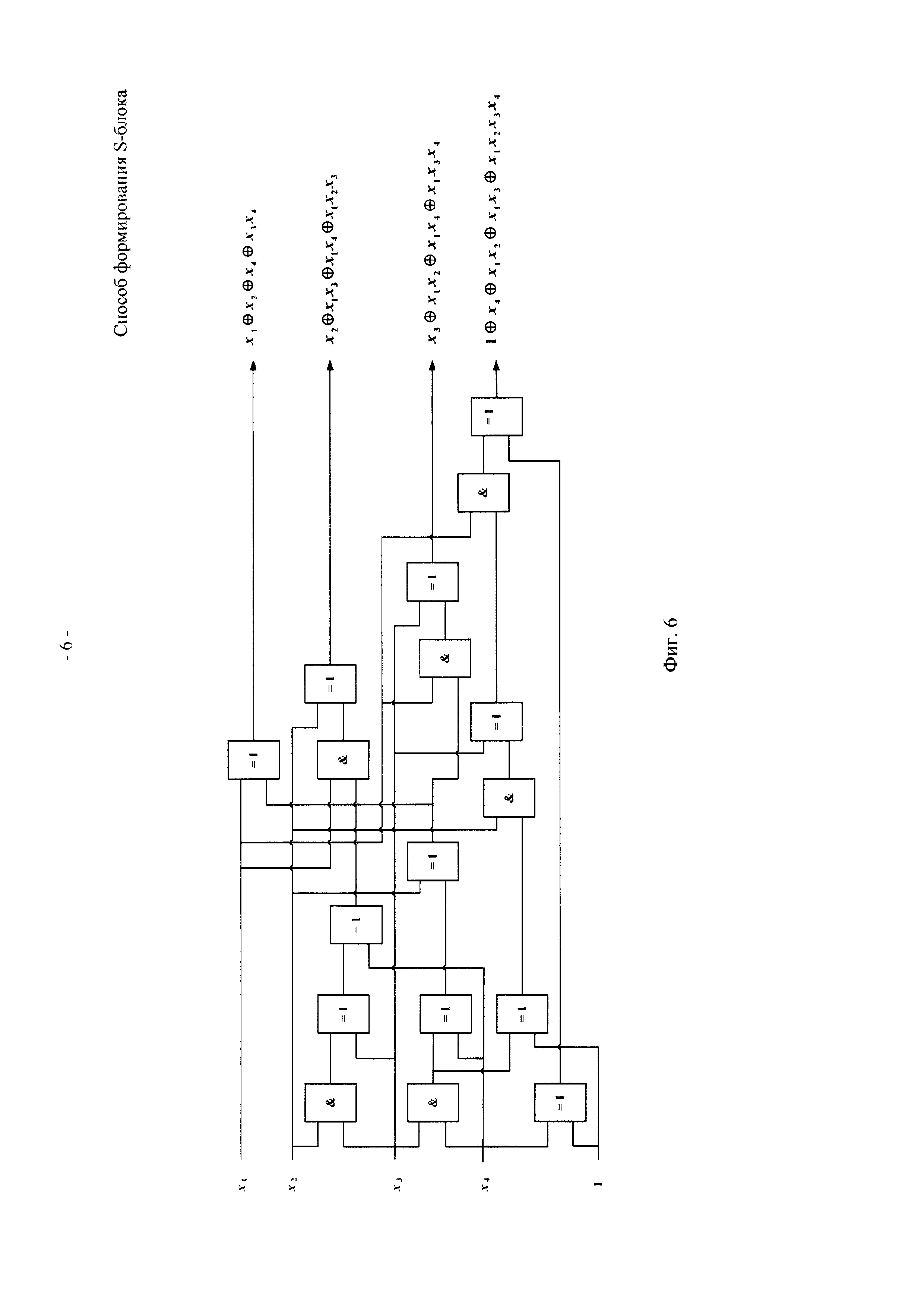
На фиг. 6 показана финальная логическая схема для примера реализации способа.
Осуществление изобретения
Рассмотрим пример реализации предложенного способа для S-блока, имеющий 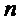 = 4 входов и
= 4 входов и 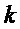 = 4 выходов и заданного следующими многочленами Жегалкина от четырех переменных
= 4 выходов и заданного следующими многочленами Жегалкина от четырех переменных 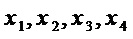
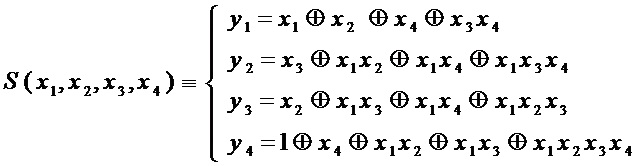
Прямой способ реализации этого S-блока требует 11 операций & для формирования мономов 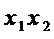 ,
, 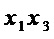 ,
, 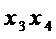 ,
, 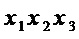 ,
, 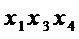 ,
, 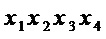 и 13 операций
и 13 операций 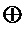 для составления из них многочленов.
для составления из них многочленов.
Рассмотрим применение предлагаемого способа в условиях, когда схемотехнические затраты на реализацию операций & и ⊕ совпадают, т.е. 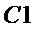 =
= 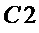 = 1.
= 1.
Число общих мономов у любой пары многочленов не превышает 1, поэтому способ из прототипа не дает выигрыша по количеству операций, т.е. не приводит к снижению схемотехнических затрат.
В предлагаемом способе этому S-блоку соответствуют исходные значения:
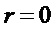
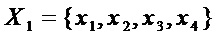
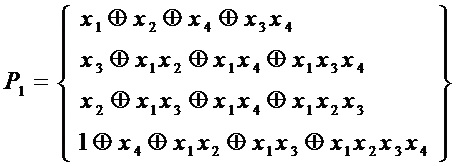
У любых двух многочленов из множества 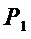 совпадает не более одного монома, что при
совпадает не более одного монома, что при 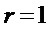 на этапе А1 (согласно обозначению в формуле изобретения), соответствует тому, что
на этапе А1 (согласно обозначению в формуле изобретения), соответствует тому, что 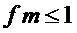 . Поэтому на этапе А1 после присвоения значения
. Поэтому на этапе А1 после присвоения значения 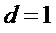 выполняют переход на этап А2, где вычисляют значение
выполняют переход на этап А2, где вычисляют значение 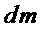 , характеризующую сложность прямой реализации множества многочленов
, характеризующую сложность прямой реализации множества многочленов 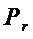
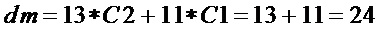
и величину имеющегося снижения сложности

С этапа А3 до этапа А4 по очереди перебирают переменные 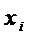 из множества
из множества 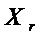 . Для выбранного значения
. Для выбранного значения 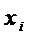 каждый многочлен
каждый многочлен 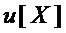 из
из 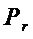 представляют в одном из 2-х вариантов:
представляют в одном из 2-х вариантов:
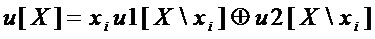
или
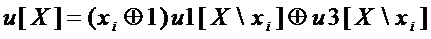 ,
,
в записи которого меньше операций 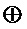 . Для полученного разложения многочленов
. Для полученного разложения многочленов 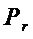 по переменной
по переменной 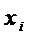 подсчитывают значение
подсчитывают значение 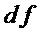 , характеризующую снижение сложности прямой реализации множества многочленов
, характеризующую снижение сложности прямой реализации множества многочленов 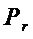 за счет перехода к прямой реализации выделенных компонент разложения с последующим составлением исходных многочленов по выбранным формулам.
за счет перехода к прямой реализации выделенных компонент разложения с последующим составлением исходных многочленов по выбранным формулам.
Для рассматриваемого множества многочленов 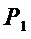 перебор переменных
перебор переменных 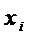 дает следующие результаты разложения многочленов и соответствующие им оценки сложности использования такого разложения:
дает следующие результаты разложения многочленов и соответствующие им оценки сложности использования такого разложения:
Для 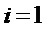 :
:
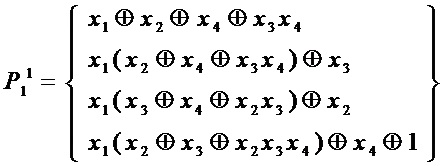
сложность
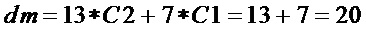
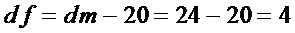
Для 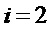 :
:
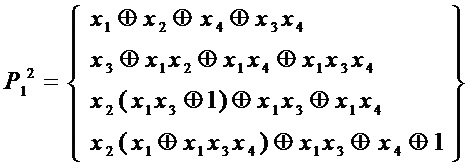
сложность
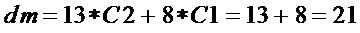
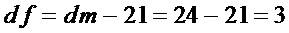
Для 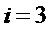 :
:
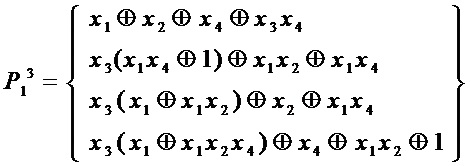
сложность
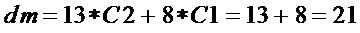
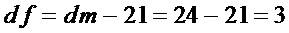
Для 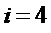 :
:
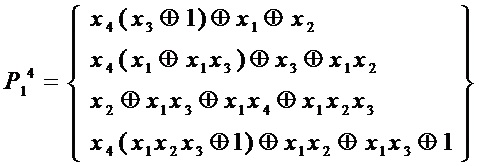
сложность
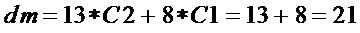
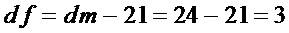
Наибольшее снижение сложности (значение 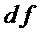 ) имеет место при
) имеет место при 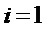 . Поэтому на этапе А4 при переходе на этап А1 при
. Поэтому на этапе А4 при переходе на этап А1 при 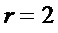 :
:
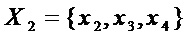
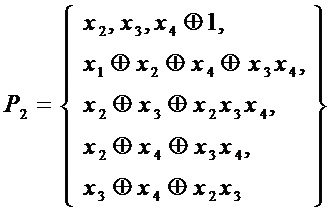
Для множества многочленов 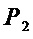 максимальная общая часть двух многочленов состоит из 3-х мономов
максимальная общая часть двух многочленов состоит из 3-х мономов 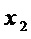 ,
, 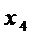 ,
, 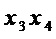 . Поэтому при переходе на этап А2 вычисляемые параметры имеют значения:
. Поэтому при переходе на этап А2 вычисляемые параметры имеют значения:
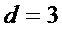
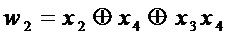

На этапе А2 вычисляют сложность прямой реализации множества многочленов 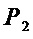
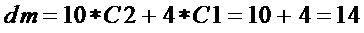
и снижение сложности за счет выделения общего слагаемого 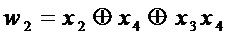
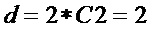
На этапах с А3 по А4 разложение многочленов множества 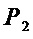 по переменным
по переменным 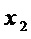 ,
, 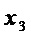 ,
, 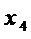 из множества
из множества 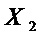 дает следующие оценки сложности использования данного разложения по сравнению с сложностью прямой реализации множества
дает следующие оценки сложности использования данного разложения по сравнению с сложностью прямой реализации множества 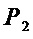
Для 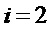 :
:
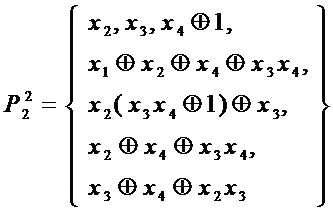
сложность
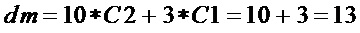
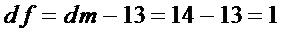
Для 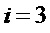 :
:
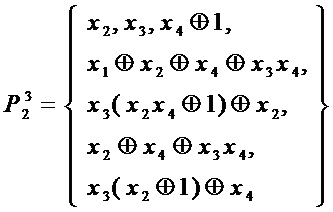
сложность
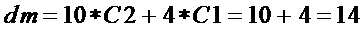
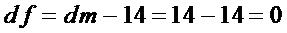
Для 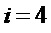 :
:
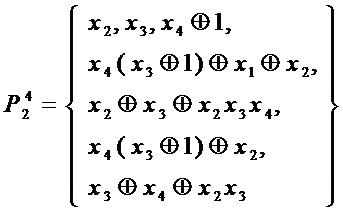
сложность
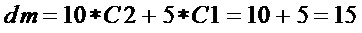

Наибольшее снижение сложности (значение 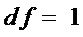 ) имеет место при
) имеет место при 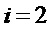 , что меньше снижения сложности (значение
, что меньше снижения сложности (значение 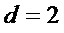 ) при выделение многочлена
) при выделение многочлена 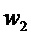 .
.
Поэтому на этапе А4 при переходе на этап А1 при 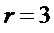 вычисляемые параметры имеют следующие значения:
вычисляемые параметры имеют следующие значения:
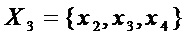
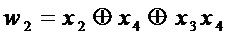

Число общих мономов у любой пары многочленов из множества 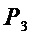 не превышает 1, поэтому при переходе на этап А3 при
не превышает 1, поэтому при переходе на этап А3 при 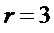 вычисляемые параметры имеют следующие значения
вычисляемые параметры имеют следующие значения
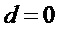
и сложность прямой реализации 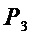
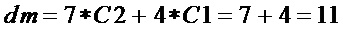
На этапах с А3 по А4 разложение многочленов множества 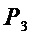 по переменным
по переменным 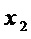 ,
, 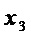 ,
, 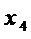 из множества
из множества 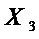 дает следующие оценки сложности использования данного разложения по сравнению со сложностью прямой реализации множества
дает следующие оценки сложности использования данного разложения по сравнению со сложностью прямой реализации множества 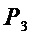 .
.
Для 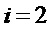 :
:
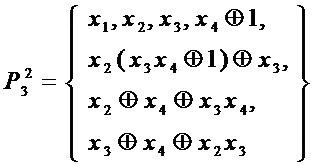
сложность
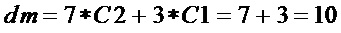
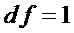
Для 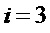 :
:
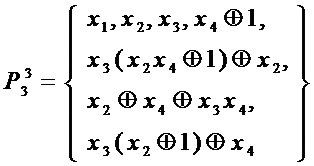
сложность
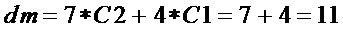
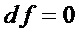
Для 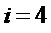 :
:
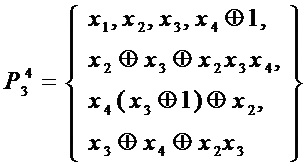
сложность
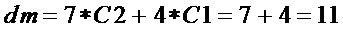
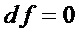
Наибольшее снижение сложности имеет место при 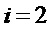 . Поэтому на этапе А4 при переходе на этап А1 при
. Поэтому на этапе А4 при переходе на этап А1 при 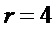 вычисляемые параметры имеют следующие значения:
вычисляемые параметры имеют следующие значения:
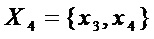
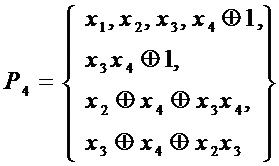
Число общих мономов у любой пары многочленов из множества 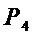 не превышает 1, поэтому переходят на этап А3 - к анализу разложений многочленов множества
не превышает 1, поэтому переходят на этап А3 - к анализу разложений многочленов множества 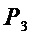 по переменным
по переменным 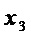 ,
, 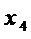 из множества
из множества 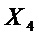 .
.
Никакой из двух вариантов разложения не приводит к снижению оценки сложности, поэтому формируют множество мономов
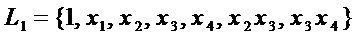
и переходят к этапу А5 при 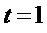 .
.
На этапе А5 при 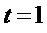 максимальное число общих переменных, равное 1, имеют мономы
максимальное число общих переменных, равное 1, имеют мономы 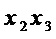 и
и 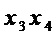 из множества
из множества 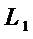 . Для этих мономов вычисления дают результат:
. Для этих мономов вычисления дают результат: 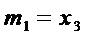 и множество мономов
и множество мономов 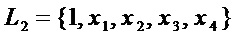 .
.
В множестве мономов 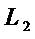 уже нет мономов с общими переменными, поэтому переходят на этап А6 - к синтезу схемы из элементов
уже нет мономов с общими переменными, поэтому переходят на этап А6 - к синтезу схемы из элементов 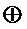 и &.
и &.
Схема для множества 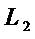 проста: входы
проста: входы 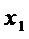 ,
, 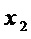 ,
, 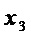 ,
, 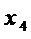 соединены с одноименными выходами
соединены с одноименными выходами 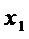 ,
, 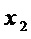 ,
, 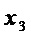 ,
, 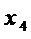 и добавлен выход постоянного сигнала 1 (фиг. 1).
и добавлен выход постоянного сигнала 1 (фиг. 1).
Переход к схеме для множества 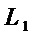 выполняют путем добавления к схеме
выполняют путем добавления к схеме 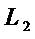 части, осуществляющей вычисления отсутствующих в
части, осуществляющей вычисления отсутствующих в 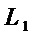 мономов
мономов 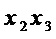 и
и 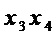 (фиг. 2).
(фиг. 2).
При переходе к схеме для множества многочленов 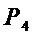 к схеме для
к схеме для 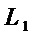 добавляют части, которые соответствуют многочленам
добавляют части, которые соответствуют многочленам 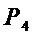 с двумя и более мономами, и которые осуществляют сложение выходов мономов этого многочлена в схеме
с двумя и более мономами, и которые осуществляют сложение выходов мономов этого многочлена в схеме 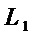 для формирования входа, соответствующего данному многочлену (фиг. 3).
для формирования входа, соответствующего данному многочлену (фиг. 3).
При переходе от схемы для множества многочленов 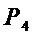 к схеме для множества многочленов
к схеме для множества многочленов 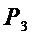 добавляют часть, реализующую многочлен
добавляют часть, реализующую многочлен 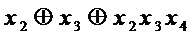 : добавляют операцию & над выходом, соответствующем многочлену
: добавляют операцию & над выходом, соответствующем многочлену 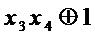 , и входом переменной
, и входом переменной 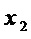 и соединяют операцией ⊕ результат данной операции & с входом переменной
и соединяют операцией ⊕ результат данной операции & с входом переменной 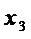 (фиг. 4).
(фиг. 4).
При переходе от схемы для множества многочленов 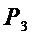 к схеме для множества многочленов
к схеме для множества многочленов 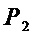 добавляют часть, реализующую многочлен
добавляют часть, реализующую многочлен 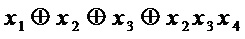 : соединяют через операцию ⊕ выход, соответствующий многочлену
: соединяют через операцию ⊕ выход, соответствующий многочлену 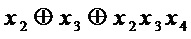 , и вход переменной
, и вход переменной 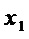 (фиг. 5).
(фиг. 5).
Переход от схемы для множества многочленов 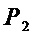 к схеме для множества многочленов
к схеме для множества многочленов 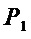 полностью аналогичен переходу от схемы
полностью аналогичен переходу от схемы 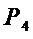 к схеме
к схеме 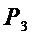 : добавляются части, являющиеся произведением (в смысле операции &) одного из выходов и одной из входящих переменных с последующим суммированием (в смысле операции ⊕) с другим выходом (фиг. 6).
: добавляются части, являющиеся произведением (в смысле операции &) одного из выходов и одной из входящих переменных с последующим суммированием (в смысле операции ⊕) с другим выходом (фиг. 6).
В полученной финальной схеме реализации S-блока (фиг. 8) использовано 11 операций ⊕ и 6 операций &, что меньше исходных значений 13 операций ⊕ и 11 операций &.
Таким образом, предлагаемый способ уменьшает схемотехнические затраты – количество элементов, реализующих операции & и ⊕ при формировании заданного S-блока.
В случае исходного S-блока большой размерности процедуру построения логической схемы, согласно предложенному способу, целесообразно автоматизировать путем составления программы для ЭВМ, что вполне может выполнить специалист по программированию (программист) на основе знания действий способа.
Последующая схемотехническая реализация полученного S-блока может быть осуществлена известными методами, предпочтительной формой для использования в современной компьютерной технике является реализация на ПЛИС, но это необязательно. Конкретный выбор варианта схемотехнической реализации зависит от разработчика.
Источники информации, принятые во внимание при формировании заявки
1. Самофалов К.Г. и др. Прикладная теория цифровых автоматов (учебник), Киев, Вища Школа, 1987.
2. Патент РФ № 2331937, приоритет от 24.08.2006 г.
3. Патент США № 7421076, приоритет от 17.09.2003 г.
4. Спирин П.А. Спирина М.С. Дискретная математика (учебник), Издательский центр “Академия”, 2004